ВЕТВЯЩИЙСЯ ПРОЦЕСС

ВЕТВЯЩИЙСЯ ПРОЦЕСС - случайный процесс, описывающий широкий круг явлений, связанных с размножением и превращением к.-л. объектов (напр., частиц в физике, молекул в химии, особей к.-л. популяции в биологии и т. п.). Основным математич. предположением, выделяющим класс В. п., является предположение независимости размножения частиц друг от друга.

Однородный во времени В. п. μ(t) с однотипными частицами определяется как марковский процесс со счетным числом состояний 0, 1, 2, ..., переходные вероятности Р_ij(t) к-рого удовлетворяют дополнительному условию ветвления:

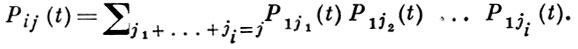
Состояния 0, 1, 2, ... в В. п. интерпретируются как числа частиц. Вероятность Р_ij(t) равна вероятности

P{μ(t + t₀) = j | μ(t₀) = i}

того, что i частиц за время t превращаются в j частиц. Основным аналитич. аппаратом В. п. являются производящие функции

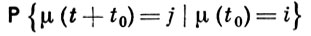
(2)

Из условия ветвления (1) вытекает равенство

F(t + τ; s) = F(t; Р(τ; s)). (3)

В В. п. с дискретным временем (в. п. с д. в.) t принимает целые неотрицательные значения, и из (3) следует, что F(t; s) есть t-кратная итерация функции P(s) = P(1; s). Такой процесс иногда наз. процессом Гальтона-Ватсона. В В. п. с непрерывным временем (в. п. с н. в.) предполагается, что t ∈ [0, ∞), и существует правая производная

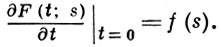
Из (3) следует, что F(t; s) удовлетворяет дифференциальному уравнению

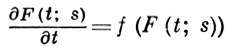
(4)

и начальному условию F(0, s) = s.

Если A = F'(1) и a = f(1) конечны, то математич. ожидание Еμ(t) числа частиц μ(t) (при условии μ(0) = 1) равно A^t для в. п. с д. в. и равно e^at для в. п. с н. в. В зависимости от значения параметров А или а В. п. подразделяются на докритические (А < 1, а < 0), критические (A = 1, а = 0) и надкритические (A > 1, а > 0). Основным свойством, определяющим эту классификацию, является поведение Еμ(t) при t → ∞.

Ниже исключаются из рассмотрения тривиальные случаи F(s) ≡ s и f(s) ≡ 0, когда

Р{μ(t) = 1 | μ(0) = 1} ≡ 1.

Вероятность вырождения равна 1 в докрптич. и критич. В. п. и меньше 1 в надкритич. В. п. Если Еμ(t) ln μ(t) < ∞, то в докритич. В. п. вероятность продолжения процесса Р{μ(t) > 0} при t → ∞ асимптотически ведет себя как KЕμ(t), где К - положительная константа. В критич. В. п. с конечным Еμ²(t) при t → ∞ имеет место асимптотика

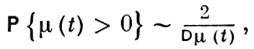
где Dμ(t) = Bt в в. п. с д. в. и Dμ(t) = bt в в. п. с н. в., B = F''(1), b = f''(1). Более детальное изучение асимптотич. поведения распределения μ(t) при t → ∞ показывает, что условный закон распределения

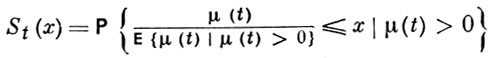
(5)

при t → ∞ слабо сходится к предельному распределению S(x), если конечны нек-рые моменты μ(t). В докритич. В. п. предельный закон S(х) дискретен, а в остальных случаях абсолютно непрерывен. Особенно интересен случай критич. В. п., для к-рого предельный закон S(х) показательный

S(x) = 1 - е^-x, х ≥ 0. (6)

Распределение (6) является предельным также и для В. п., близких к критическим. Точнее, если рассматривать класс производящих функций F(s) или f(s) с ограниченной 3-й производной F'''(1), f'''(1) и с F''(1) ≥ B₀ > 0, f'' (1) ≥ b₀ > 0, то

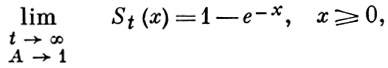
где S_t(x) определяется формулой (5). Явления, возникающие при t → ∞ в В. п., близких к критическим, наз. переходными.

Другой моделью В. п. является Беллмана-Xарриса процесс, в к-ром каждая частица имеет случайное время жизни с функцией распределения G(t). В конце жизни частица оставляет потомство численности n с вероятностью q_n,

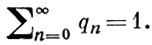
Времена жизни и численности потомства разных частиц независимы. Пусть в начальный момент t = 0 была одна частица нулевого возраста. Тогда производящая функция F(t; s) числа частиц μ(t) в момент t, определяемая формулой (2), удовлетворяет нелинейному интегральному уравнению

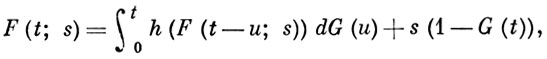
(7)

где

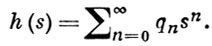
В частном случае, когда G(t) - вырожденная функция распределения, процесс Беллмана-Харриса есть в. п. с д. в.; когда же G(t) - показательная функция распределения, получается в. п. с п. в. В общем случае процесс Беллмана-Харриса - это немарковский В. п.

Другое усложнение В. п. связано с зависимостью частиц от положения в пространстве. Пусть, напр., частицы независимо друг от друга совершают броуновское движение в r-мерной области G с поглощающей границей ∂G. Частица, находящаяся внутри области G, за время Δt → 0 с вероятностью

р_nΔt + о(Δt), n ≠ 1,

превращается в n частиц, к-рые начинают независимо друг от друга блуждать по броуновским траекториям из точки их рождения. Пусть μ_xt(А) равно числу частиц в множестве А в момент t, если в начальный момент 0 была одна частица в точке x ∈ G. Производящий функционал

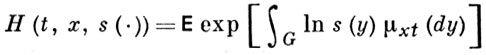
удовлетворяет квазилинейному параболич. уравнению

ΔH + f(H) = 0 (8)

с начальным условием H(0, х, s(⋅)) = s(x) и граничным условием

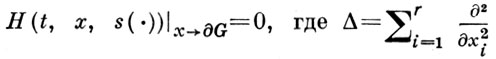
- оператор Лапласа, а f(s) = ∑_np_nsⁿ, p₁ = -∑_n≠1 p_n.

В общем случае В. п. предполагается, что размножающиеся частицы характеризуются к.-л. параметрами, к-рые можно интерпретировать как возраст, положение частицы в пространстве, тип, размер или энергию частицы и т. п. Изучение таких процессов ведется с помощью производящих функций или функционалов, для к-рых выводятся нелинейные дифференциальные или интегральные уравнения, обобщающие уравнения (4), (7), (8). Можно дать следующее общее описание таких моделей В. п. Пусть в нек-ром фазовом пространстве X независимо друг от друга по закону марковского процесса блуждают частицы. Предполагается, что случайное время жизни частицы есть марковский момент, зависящий от ее траектории. В конце своей жизни частица производит новые частицы, к-рые по к.-л. вероятностному закону распределяются по фазовому пространству X. Новые частицы эволюционируют независимо друг от друга аналогичным образом. В пространстве целочисленных мер, определяемых численностями частиц в подмножествах X, так построенный В. п. является марковским. Однако В. п. часто рассматриваются в более простых редуцированных пространствах. В этом случае многие из них становятся немарковскими.

В большей части приведенных выше моделей сохраняет смысл подразделение процессов на докритические, критические и надкритические В. п. При этом в более сложной обстановке сохраняются многие свойства, установленные для простых В. п., описываемых уравнением (4). В частности, в критич. процессах, как правило, в качестве предельного распределения для (5) (при соответствующей нормировке) возникает показательное распределение (6).

В. п. находят применение при расчетах различных реальных биологич., генетич., физич., химич. или технич. процессов. В реальных процессах часто нарушается условие независимости размножения различных частиц и, наоборот, при размножении имеется взаимодействие частиц. Так обстоит дело во многих биологич. процессах размножения, в процессах распространения эпидемий (см. Эпидемии процессы), в бимолекулярных химич. реакциях и т. п. Однако начальные стадии развития таких процессов можно рассчитывать с помощью соответственно подобранных моделей В. п. Это делается в тех случаях, когда в среде имеется не очень много активных частиц, к-рые при малых концентрациях почти не встречаются друг с другом, а изменения состояния системы происходят при встречах этих активных частиц с частицами среды. В процессах эпидемии, напр., такими «активными частицами» можно считать больных индивидуумов. В генетике с помощью В. п. можно рассчитывать, напр., явления, связанные с мутациями. Ветвящийся процесс с конечным числом типов частиц может служить моделью при расчетах цепных реакций; ветвящийся процесс с диффузией частиц _ моделью нейтронных процессов в ядерных реакторах. Явления, возникающие в ливнях космич. лучей, также могут изучаться с помощью В. п. В телефонии расчет нек-рых систем с ожиданием сводится к моделям В. п.

См. также Ветвящийся процесс со случайной средой, Ветвящийся процесс с иммиграцией, Ветвящихся процессов регулярность.

Лит.: [1] Севастьянов Б. А., Ветвящиеся процессы, М., 1971; [2] Athreya К. В., Ney P. Е., Branching Processes, В.-Hdlb., N. Y., 1972.

Б. А. Севастьянов

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.