ВЕТВЛЕНИЯ ТОЧКА

ВЕТВЛЕНИЯ ТОЧКА, особая точка многозначного характера,- изолированная особая точка а аналитич. функции f(z) одного комплексного переменного z такая, что аналитическое продолжение к.-л. элемента функции f(z) вдоль замкнутого пути, охватывающего а, приводит к новым элементам f(z). Точнее, а наз. В. т., если существуют: 1) кольцо V = {z; 0 < |z- а| < ρ}, в к-ром f(z) аналитически продолжается по любому пути; 2) точка z₁ ∈ V и к.-л. элемент функции f(z), представленный степенным рядом

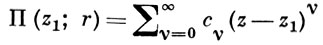
с центром z₁ и радиусом сходимости r > 0, аналитич. продолжение к-рого вдоль окружности |z - a| = |z₁ - а|, проходимой один раз, напр. в положительном направлении, приводит к новому элементу П'(z₁; r'), отличающемуся от П(z₁; r). Если после нек-рого минимального числа k > 1 таких обходов снова получается исходный элемент П(z₁; r), то это же самое будет иметь место для всех элементов ветви аналитической функции f(z), определяемой в V элементом П(z₁; r). В таком случае а является В. т. конечного порядка k - 1 для указанной ветви. В проколотой окрестности V В. т. а конечного порядка эта ветвь представима в виде обобщенного ряда Лорана, или ряда Пюизё:

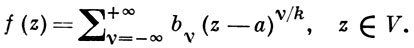
(1)

Если а = ∞ - бесконечно удаленная В. т. конечного порядка, то в нек-рой окрестности V' = {z; |z| > ρ} данная ветвь f(z) представима в виде аналога ряда (1):

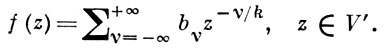
(2)

Поведение римановой поверхности R функции f(z) над В. т. конечного порядка а характеризуется тем, что над а соединяются вместе к листов той ветви f(z), к-рая определяется элементом П(z₁; r). При этом поведение других ветвей R над а может быть совершенно иным.

Если в ряде (1) или (2) среди коэффициентов b_ν с отрицательными индексами ν имеется лишь конечное число отличных от нуля, то а - алгебраическая точка ветвления, или алгебраическая особая точка. Такая В. т. конечного порядка характеризуется также тем, что при любом стремлении z → а в V или V' значения всех элементов ветви, определяемой П(z₁; r), стремятся к определенному конечному или бесконечному пределу.

Пример: f(z) = ^k√z, k > 1 - натуральное число, а = 0, ∞.

Если в ряде (1) или (2) имеется бесконечно много ненулевых коэффициентов b_ν с отрицательными индексами ν, то В. т. конечного порядка а относится к классу трансцендентных В. т. Пример:

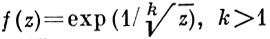
- натуральное число, а = 0.

Наконец, если ни при каком числе последовательных обходов нельзя возвратиться к исходному элементу, то а наз. логарифмической точкой ветвления, или В. т. бесконечного порядка, и также относится к трансцендентным В. т. Пример: f(z) = Ln z, а = 0, ∞. Над логарифмич. В. т. соединяются бесконечно много листов той ветви f(z), к-рая определяется элементом П(z₁; r).

В случае аналитич. функции многих комплексных переменных f(z), z = (z₁, ..., z_n), n ≥ 2, точка а пространства ℂⁿ или ℂРⁿ наз. В. т. порядка m, 1 ≤ m ≤ ∞, если она является В. т. порядка m, вообще говоря, многолистной голоморфности области функции f(z). В отличие от случая n = 1, при n ≥ 2 В. т., как и другие особые точки аналитических функций многих комплексных переменных, не могут быть изолированными.

Лит.: [1] Маркушевич А. И., Теория аналитических функций, 2 изд., т. 2, М., 1968, гл. 8; [2] Фукс Б. А., Теория аналитических функций многих комплексных переменных 2 изд., М., 1962, ч. 1, гл. 2.

Е. Д. Соломенцев.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.