ВЕТВЛЕНИЕ РЕШЕНИЙ

ВЕТВЛЕНИЕ РЕШЕНИЙ нелинейных уравнений - явление перехода нек-рого решения нелинейного уравнения в несколько решений (пли полное его исчезновение) при малых изменениях параметров. Более точно, пусть нелинейное уравнение

F(x, λ) = 0 (*)

с (не обязательно числовым) параметром λ имеет при фиксированном значении λ₀ решение х₀. Тогда при значениях λ, близких к λ₀, уравнение (*) может иметь несколько (более одного) решений х(λ), близких к х₀. В этих случаях говорят, что происходит ветвление решения х₀, а пара (х₀, λ₀) наз. точкой ветвления уравнения (*).

Пример: Уравнение х² - λ = 0, где х и λ - комплексные переменные, имеет точку ветвления (х₀, λ₀) = (0, 0), ибо существует двузначное решение х = √λ, т. е. решение х = 0 (при λ = 0) разветвляется при малых λ ≠ 0 на два малых нетривиальных решения.

Современная теория В. р. основывается на идеях А. М. Ляпунова [1] и Э. Шмидта [2] и наиболее развита для нелинейных уравнений в банаховых пространствах.

Пусть Е₁ и Е₂ - комплексные банаховы пространства, x ∈ E₁, λ - комплексное переменное, a F(x, λ) -нелинейный оператор, непрерывный вместе с Фреше производной F_x(x, λ) в окрестности Ω точки (х₀, λ₀), отображающий Ω в окрестность нуля пространства Е₂ и такой, что F(x₀, λ₀) = 0, a F_x(x₀, λ₀) ≡ В - Фредгольма оператор.

Задача состоит в том, чтобы найти в шаре ||х - х₀|| < r достаточно малого радиуса r все решения уравнения (*), непрерывные при |λ - λ₀| < ρ, где ρ также достаточно мало. Иными словами, это есть задача локального продолжения решения х₀ по параметру λ. Если существует обратный оператор В^-1, то задача имеет единственное решение х(λ), причем х(λ₀) = х₀. Если же В^-1 не существует, то нуль-пространство N(В) оператора В имеет размерность n ≥ 1. В этом случае задача может быть сведена к аналогичной конечномерной задаче. Пусть через Р обозначен проектор Е₁ на N(В), а через I - Q - проектор Е₂ на область значений оператора В, где I - тождественный оператор. Уравнение (*) может быть записано в виде системы

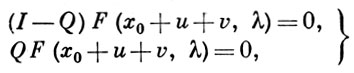
где u = (I - P)(x - x₀), v = P(x - x₀). Из первого уравнения системы определяется неявный оператор u = f(v, λ). В результате его подстановки во второе уравнение системы получается уравнение

QF(x₀ + f(v, λ) + v, λ) = 0

для определения v; оно наз. уравнением разветвления. Полное решение задачи о нахождении в шаре ||v|| < r достаточно малого радиуса r всех решений v(λ) уравнения разветвления, непрерывных при |λ - λ₀| < ρ (где ρ достаточно мало), приводит к полному решению исходной задачи, ибо всякое ее решение представимо в виде

x(λ) = x_c + v(λ) + f[v(λ), λ],

где v - нек-рое решение уравнения разветвления.

Пусть F(x, λ) - аналитический оператор в Ω. Выбор базисов в n-мерных подпространствах PE₁ = N(B) и QE₂ позволяет записать уравнение разветвления в виде системы

ℒ_i (ξ₁, ..., ξ_n, λ) = 0, i = 1, ..., n,

ℒ_i, i = 1, ..., n - аналитич. функции в точке (0, ..., 0, λ₀), причем все частные производные ∂ℒ_i/∂ξ_j обращаются в нуль в этой точке. Исследование этой системы может осуществляться при помощи теории исключения, метода Ньютона диаграммы и др. методов (см. [3]-[5]). При n = 1 полный анализ осуществляется методом диаграммы Ньютона. Применительно к исследованию уравнения разветвления, а значит и исходной задачи, возможны лишь следующие три случая: а) задача не имеет решений; б) задача имеет конечное число решений и все они представимы сходящимися рядами по целым или дробным степеням разности λ - λ₀; в) задача имеет конечное число семейств решений, каждое из к-рых зависит от конечного числа свободных малых параметров, и, быть может, конечное число решений, указанных в б).

Для того чтобы имел место случай б), достаточно, чтобы х₀ было изолированным решением уравнения F(x, λ₀) = 0. В случае б) решения удобно искать методом неопределенных коэффициентов в виде

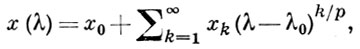
где x_k - коэффициенты, подлежащие определению, а возможные значения р могут быть предварительно найдены с помощью уравнения разветвления. Подстановка такого ряда в (*) приводит к рекуррентной системе для нахождения х₁, х₂, ... . При этом получаются задачи вида Bx_k = H(x₁, ..., x_k-1) и каждое х_k определяется с точностью до n произвольных постоянных, к-рые определяются из требований разрешимости последующих уравнений. Все полученные ряды сходятся в нек-рой окрестности точки λ₀. Оценка снизу радиуса окрестности может быть получена с помощью построения мажорант (см. [6]).

Для того чтобы имел место случай в), необходимо, чтобы х₀ было неизолированным решением уравнения F(x, λ₀) = 0. Здесь применение метода неопределенных коэффициентов может привести к расходящимся рядам (формальным решениям). Если задача инвариантна относительно непрерывной группы линейных операторов в Е₁, то в ряде случаев использование групповых соображений позволяет уменьшить число уравнений и неизвестных в уравнении разветвления и тем самым упростить задачу или даже свести ее к случаю б) (см. [7], [8]).

Уравнение (*) может иметь также решения, определенные лишь при λ = λ₀. Эти решения возможны только тогда, когда х₀ - неизолированное решение уравнения F(х, λ₀) = 0; они находятся при помощи уравнения разветвления при λ = λ₀. Определение всех его многонараметрич. семейств решений приводит к определению всех решений уравнения (*) с λ = λ₀.

В случае вещественных пространств Е₁ и Е₂ уравнение разветвления изучается в комплексной области, а затем отбираются вещественные решения. Нек-рые из них могут оказаться определенными в полуокрестностях точки λ₀.

Изложенная методика частично применима также в случаях, когда F(x, λ) - достаточно гладкий оператор, В - нётеров оператор, а параметр λ - элемент еще одного банахова пространства Е (точки ветвления могут заполнять в Е линии и поверхности). Этим же способом исследуются нек-рые близкие задачи: задача отыскания больших решений (уравнение (*) может иметь решения х(λ) → ∞ при λ → λ₀), задача ветвления собственных значений и собственных элементов линейных операторов и др. (см. [3]). Частный случай, когда

Е₁ = Е₂, F(x, λ) ≡ х - Ф(х, λ), Ф(0, λ) ≡ 0

исследовался также топологическими, вариационными методами и методами, использующими конусы в банаховом пространстве. В этом круге вопросов значительную роль играет понятие точки бифуркации. Встречаются также задачи о ветвлении решений, не укладывающиеся в описанную выше схему. Это, напр., задачи для дифференциальных уравнений с вырождением (см. [9], [10]) и задачи о длинных и уединенных волнах (см. [11]).

Лит.: [1] Ляпунов А. М., О фигурах равновесия, мало отличающихся от эллипсоидов, вращающейся однородной кассы жидкости, Собр. соч., т. 4, М., 1959; [2] Schmidt Е., «Math. Ann.», 1908, Bd 65, S. 370-99; [3] Вайнберг M. М., Треногий В. А., Теория ветвления решений нелинейных уравнений, М., 1969; [4] Вайнберг М. М., Треногий В. А., «Успехи матем. наук», 1962, т. 17, в. 2; [5] Красносельский М. А. [и др.], Приближенное решение операторных уравнений, М., 1969; [6] Ахмедов К. Т., «Успехи матем. наук», 1957, т. 12, в. 4, с. 135-53; [7] Юдович В. И., «Прикл. матем. и механ.», 1967, т. 31, в. 1, с. 101-11; [8] Логинов Б. В., Треногин В. А., «Докл. АН СССР», 1971, т. 197, №1; [9] Ахмедов К. Т. там же, 1957, т. 115, № 1; [10] Сидоров Н. А., «Дифферент уравнения», 1967, т. 3, № 9; [11] Тер-Крикоров А. М., Треногий В. А., там же, т. 3, № 3.

В. А. Треногий.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.