ВЕСОВОЕ ПРОСТРАНСТВО

ВЕСОВОЕ ПРОСТРАНСТВО, весовой класс, пространство с весом,- пространство функций, имеющих конечную норму (или полунорму) с нек-рым функциональным множителем - весом. При этом норма (полунорма) функции наз. в этом случае весовой нормой (полунормой), а вес наз. также весовой функцией нормы (полунормы). Введение веса позволяет расширять и сужать обычные невесовые функциональные нормированные и полунормированные пространства, состоящие из функций, имеющих бесконечную обычную безвесовую норму (полунорму). Напр., В. п. C_φ(E) (где φ - весовая функция), норма в к-ром определяется формулой

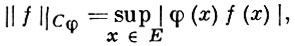
при соответствующем выборе функции φ может быть как шире, так и уже пространства С(Е) с обычной нормой

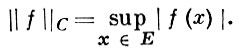
Так, в пространство C_x(0, 1) с нормой

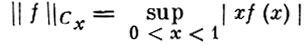
входят нек-рые неограниченные функции, и оно содержит в себе пространство С(0, 1) ограниченных на интервале (0, 1) функций в качестве собственного подпространства. Наоборот, пространство C_1/x(0, 1) с нормой

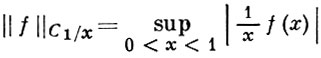
содержится в пространстве С (0, 1) как собственное подпространство. Другой пример: полунормированное пространство с весовой полунормой 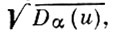где u = u(х, у) и

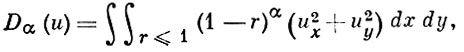
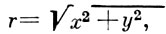
при α > 0 содержит в себе как собственное подпространство пространство функций с безвесовой полунормой 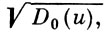, а при α < 0 содержится в нем как собственное подпространство.

Наиболее часто рассматривается случай, когда весовая функция стремится к нулю или к бесконечности при приближении к заданному многообразию, к-рое может вырождаться в точку, в частности в бесконечно удаленную. В. п. естественным образом возникают как в теории функций при изучении обычных (невесовых) функциональных пространств, так и в приложениях теории функций, напр. к теории краевых задач для уравнений с частными производными.

Основным вопросом при изучении В. п. является получение для них вложения теорем. В теоремах вложения одного типа устанавливается оценка нормы функции через ее норму в другом В. п., причем в обеих нормах фигурирует одна и та же область задания функции. К теоремам такого типа относятся теоремы об эквивалентности норм в В. п., в частности теоремы о нормах, определяемых с помощью преобразования Фурье - Бесселя. Сюда же относятся оценки в соответствующих пространствах весовых норм младших производных, в частности самой функции через (весовые) нормы старших производных. С помощью этих теорем можно, напр., определить с каким весом суммируема функция в данной области, если все ее старшие производные принадлежат данному В. п. В теоремах вложения другого типа даются оценки тех или иных норм следов функций на многообразиях меньшего числа измерений через их весовые нормы.

Важный класс В. п. составляют пространства функций, у к-рых абсолютные величины всех их производных до какого-то порядка суммируемы в определенной степени с весом степенного характера. В этом случае вложения В. п. изучены наиболее полно. Напр., пусть В. п. W^l_p, a(Eⁿ| ∞) состоит из функций f, имеющих на n-мерном евклидовом пространстве Еⁿ все обобщенные производные D^k₀f, k = (k₁, ..., k_n), до порядка l включительно, такие, что для них конечна величина (являющаяся нормой):

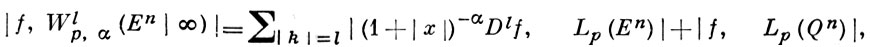
где

- единичный n-мерный шар в Еⁿ, 1 ≤ p ≤ ∞, α - действительное число, |k| = к₁ + ... + k_n. Тогда справедлива теорема вложения: если α > (n/p) - 1, 0 ≤ k ≤ l, то

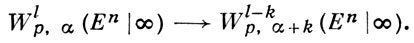
При малых α > 0 (т. е. при так наз. слабом вырождении) В. п. W^l_p,α(Еⁿ| ∞) имеют свойства, близкие к свойствам безвесовых пространств: если 0≤ α ≤(n/р) - 1, то при любом ε > 0 справедливо вложение

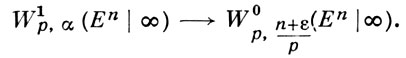
Из этого вложения при α = 0 следует, напр., что Дирихле интеграл

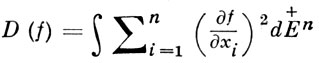
(где ⁺Еⁿ = {х : х_n > 0} - полупространство), не будучи полуограниченным снизу как функционал над пространством функций, принадлежащих L₂(⁺Еⁿ) и обращающихся в нуль на гиперплоскости Е^n-1 = {х : х_n = 0}, будет полуограничен снизу над соответствующим В. п.

Если 0 ≤ α < (n/р) - 1, то для всякой функции из В. п.W^l_p,α(Еⁿ| ∞) существует такой многочлен степени не выше l-1, что разность между ним и самой функцией стремится к нулю, когда точка стремится к бесконечности по радиусам.

Теоремы вложения о следах для В. п. являются обобщением прямых и обратных теорем вложения для обычных функциональных пространств и изучены достаточно полно для весов, имеющих порядок степени расстояния от точки области до границы области.

Теоремы вложения для В. п. применяются прежде всего в теории вырождающихся эллиптич. уравнений; они дают возможность точно сформулировать граничные задачи, указать, в зависимости от степени вырождения, какие части границы освобождаются от задания граничных условий, позволяют получить необходимые и достаточные условия (в терминах свойств граничных значений) для разрешимости ряда краевых задач; они играют важную роль при доказательстве существования и единственности решения краевых задач в соответствующем В. п. и устойчивости этого решения в смысле интеграла энергии при вариации граничных значений. В случае же неограниченных областей В. п. используются и для теории равномерно эллиптич. уравнений.

Теоремы вложения для В. п. нашли свое непосредственное применение при решении задач о наилучшем продолжении функции (или систем функций) с многообразия на все пространство таким образом, что продолженная функция бесконечно дифференцируема на дополнении к многообразию. Наилучшее продолжение здесь понимается в смысле минимального порядка роста производных при приближении точки к данному многообразию. Глобальная гладкость заданной на многообразии продолжаемой функции определяет (при достаточно гладком многообразии) максимально возможную глобальную гладкость продолжаемой функции; поэтому, начиная с нек-рого порядка, производные продолженной функции будут иметь конечную норму лишь с нек-рым весом, т. е. принадлежать соответствующему В. п.

Лит.: [1] Никольский С. М., «Успехи матем. наук». 1961, т. 16, в. 5, с. 63-114; [2] Кудрявцев Л. Д., Никольский С. М., в сб.: Некоторые проблемы математики и механики, Новосибирск, 1961, с. 87-109; [3] Кудрявцев Л. Д., «Тр. Матем. ин-та АН СССР», 1959, т. 55, с. 1-181; [4] Теория вложений классов дифференцируемых функций многих переменных, в сб.: Дифференциальные уравнения с частными производными, М., 1970, с. 38-63.

Л. Д. Кудрявцев.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.