ВЕРХНЯЯ ГРАНЬ СЕМЕЙСТВА ТОПОЛОГИЙ

ВЕРХНЯЯ ГРАНЬ СЕМЕЙСТВА ТОПОЛОГИЙ, точная верхняя грань, на множестве S -топология ξ, наименьшая из всех топологий на множестве S, содержащих каждую топологию заданного семейства (см. Сравнение топологий). Предбазу топологии ξ образует семейство всех подмножеств множества S, открытых хотя бы в одной топологии семейства .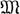

Семейство всех возможных топологий на множестве S с определенной выше операцией взятия верхней грани любого подсемейства и минимальным элементом - тривиальной топологией - есть полная решетка. В. г. с. т. наз. также индуктивным пределом семейства топологий.

Полезна следующая интерпретация В. г. с. т. Пусть

T = П{(S, ): ∈ }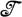

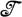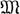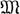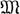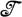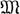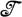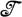- тихоновское произведение всех топологич. пространств, возникающих от наделения множества S различными топологиями из семейства . Через S* обозначим диагональ этого произведения, т.е. множество всех постоянных отображений в S (или, что то же самое, множество всех нитей {S: ∈ }, для к-рых S = S_', при всех множество S* находится в естественном взаимно однозначном соответствии с множеством S, к-рое осуществляется при проектировании множества Т на любой сомножитель. Если наделить S* топологией, индуцированной из пространства Т, и перенести эту топологию посредством указанного естественного соответствия на S, то получим верхнюю грань семейства - 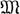. Эта интерпретация В. г. с. т. позволяет понять, что верхняя грань любого семейства хаусдорфовых топологий есть хаусдорфова топология, верхняя грань любого семейства вполне регулярных топологий есть вполне регулярная топология. Аналогичные утверждения для семейств регулярных, нормальных и паракомпактных топологий неверны. Но верхняя грань счетного семейства метризуемых топологий (со счетной базой) есть метризуемая топология (со счетной базой). Диагональ S* не замкнута, как правило, в Т, и потому верхняя грань двух бикомпактных топологий обычно не является бикомпактной.

Лит.: [1] Келли Дж. Л., Общая топология, пер. с англ., М., 1968; [2] Бурбаки Н., Общая топология. Основные структуры, пер. с франц., М., 1968.

А. В. Архангельский.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.