ВЕРХНИХ И НИЖНИХ ФУНКЦИЙ МЕТОД

ВЕРХНИХ И НИЖНИХ ФУНКЦИЙ МЕТОД - метод доказательства существования решения краевых задач для дифференциальных уравнений. Идея В. и н. ф. м. для случая обыкновенных дифференциальных уравнений усматривается в работах Дж. Пеано (G. Peano, 1880), для случая Дирихле задачи и для Лапласа уравнения - в выметании методе А. Пуанкаре (Н. Poincaré); первое полное изложение В. и н. ф. м. для этого последнего случая дано О. Перроном [1].

Пусть поставлена задача Дирихле в области G пространства Rⁿ, n ≥ 2, для линейного однородного эллиптич. уравнения 2-го порядка с непрерывными коэффициентами вида

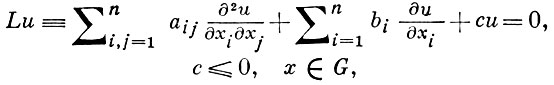
с краевым условием

u(x) = f(x), x ∈ ∂G. (2)

В. и н. ф. м. состоит в том, что, в предположении разрешимости задачи (1), (2) в малом, вводятся обобщенные супергармония, функции (соответственно субгармонические). Непрерывная на области G функция v наз. обобщенной супергармонической функцией (соответственно субгармонической) в области G, если для любого достаточно малого шара K, K̄ ⊂ G, справедливо неравенство (v)_k ≤ v (соответственно (v)_k ≥ v), где (v)_k - непрерывная на G функция, равная v вне K и на его границе и удовлетворяющая внутри К уравнению (1). Для непрерывной на границе ∂G функции f обобщенная супергармонич. (соответственно субгармоническая) функция v наз. верхней (соответственно нижней), если для x ∈ ∂G справедливо неравенство v(x) ≥ f(x) (соответственно v(x) ≤ f(x)).

Классы Ф(G, f) и Ψ(G, f) всех, соответственно, верхних и нижних функций не пусты, причем если v ∈ (G, f) и w ∈ Ψ(G, f), то v ≥ w (см. [3]). Обобщенное решение задачи Дирихле определяется как нижняя огибающая класса Ф(G, f) или как верхняя огибающая класса Ψ(G, f):

w(х) = inf{v(x); v ∈ Ф(G, f)} = sup{w(x); w ∈ Ψ(G, f)}, х ∈ G. (3)

Если граница ∂G допускает существование барьера в каждой своей точке, то u(x) = f(x) всюду на ∂G, т. е. u - классич. решение задачи Дирихле. В общем случае поведение обобщенного решения (3) эллиптич. уравнения (1) в точках границы совершенно аналогично поведению обобщенного решения уравнения Лапласа; см. Перрона метод.

В. и н. ф. м. применяется также при исследовании первой краевой задачи для линейного однородного параболич. уравнения 2-го порядка вида

с начальным условием

u(х, 0) = f(x, 0), х ∈ G,

и краевым условием

u(х, t) = f(x, t), (х, t) ∈ ∂G × [0, Т],

если ввести суперпараболические (субпараболические) функции, аналогичные по своим свойствам обобщенным супергармоническим (субгармоническим) функциям (см. [4]).

Лит.: [1] Perron О., «Маth. Z.», 1923, Bd 18, № 1/2, S. 42-54; [2] Петровский И. Г., Лекции об уравнениях с частными производными, 3 изд., М., 1961; [3] Курант Р., Уравнения с частными производными, пер. с англ., М., 1964; [4] Смирнов В. П., Курс высшей математики, т. 4, 3 изд., М., 1957.

Л. И. Камынин, Е. Д. Соломенцев.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.