ВЕРОЯТНОСТНАЯ МЕРА

ВЕРОЯТНОСТНАЯ МЕРА, вероятностное распределение, распределение вероятностей, распределение, вероятность, - действительная неотрицательная функция P на классе A подмножеств (событий) непустого множества Ω. (пространства элементарных событий), образующем борелевское поле (т. е. замкнутом относительно теоретико-множественных операций, производимых в счетном числе), такая, что

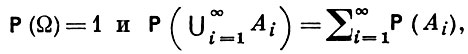
если А_i ∩ А_j = ∅ при i ≠ j (счетная аддитивность).

Примеры В. м.: 1) Ω = {1, 2}, A - класс всех подмножеств Ω, P({1}) = p({2}) = 1/2 (эта В. м. отвечает случайному эксперименту с подбрасыванием симметричной монеты; гербу ставится в соответствие 1, решетке - 2; вероятность выпадения герба (решетки) равна 1/2).;

2) Ω = {0, 1, 2, ...}, A - класс всех подмножеств Ω,

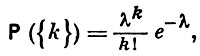
где λ > 0 (Пуассона распределение);

3) Ω = R¹, A - класс борелевских подмножеств R¹,

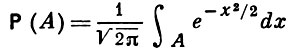
(нормальное распределение);

4) Ω = C₀[0, 1] - пространство обращающихся в нуле в нуль непрерывных действительных функций x(t) на [0, 1], A - класс борелевских подмножеств Ω относительно топологии равномерной сходимости, P -мера, однозначно определяемая формулой

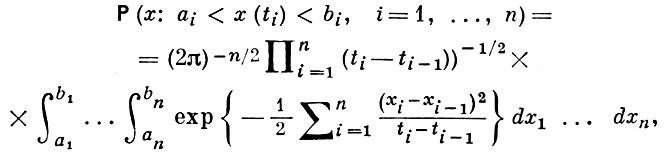
где n - произвольное натуральное число и 0 = t₀ < t₁ < ... < t_n ≤ 1 (мера Винера).

Лит.: [1] Колмогоров А. Н., Основные понятия теории вероятностей, 2 изд., М., 19 74; [2] Гнеденко Б. В., Курс теории вероятностей, 5 изд., М., 1969.

В. В. Сазонов.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.