ВЕННА ДИАГРАММА

ВЕННА ДИАГРАММА - графический способ изображения формул математич. логики, прежде всего формул исчисления высказываний. В. д. n переменных a₁, ..., a_n классич. логики высказываний представляет собой такой набор замкнутых контуров C₁, ..., C_n (гомеоморфных окружностям), к-рый разбивает плоскость на 2ⁿ областей, причем нек-рые из этих областей (например, k₁, ..., v_k, 0 ≤ k ≤ 2ⁿ) отмечены. Каждой отмеченной области V_i, 0 < i ≤ k, ставится в соответствие формула B_i = b₁ & b₂ & ... & b_n, где b_j, 0 < j ≤ n, есть a_j, если v_i лежит внутри контура C_j, и b_j есть ¬а_j в противном случае. Диаграмме в целом соответствует формула В₁ ∨ B₂ ∨ ... ∨ В_n. Напр., В. д., изображенной на рис., соответствует формула

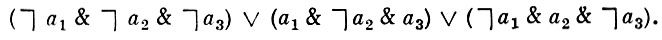
Если отмеченных областей нет (k = 0), то диаграмме сопоставляется тождественно ложная формула, напр. a₁ & ¬ a₁. В логике высказываний В. д. используются для решения проблемы разрешения, проблемы вывода всех возможных попарно неэквивалентных логич. следствий из данных посылок и др. Логика высказываний может быть построена в виде операций над В. д., сопоставленных логич. операциям.

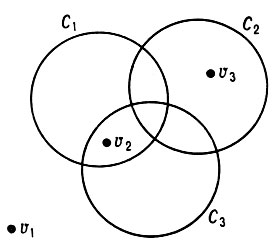
Аппарат диаграмм был предложен Дж. Венном [1] для решения задач логики классов. Метод В. д. распространен на классич. исчисление многоместных предикатов. В. д. находят применение в приложениях математич. логики и теории автоматов, в частности для решения задач теории нейронных сетей.

Лит.: [1] Venn J., Symbolic logic, 2 ed., L., 1894; [2] Кузичев А. С., Диаграммы Венна, М., 1968.

А. С. Кузичев.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.