ВЕКТОР-ФУНКЦИЯ

ВЕКТОР-ФУНКЦИЯ, векторная функция,- функция r(t) аргумента t, значения к-рой принадлежат нек-рому векторному пространству V.

В конечномерном (размерности m) векторном пространстве V задание В.-ф. эквивалентно заданию ее координат r_j(t), 1 ≤ j ≤ m, в нек-ром базисе е₁, ..., е_m пространства V:

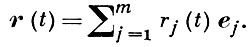
В.-ф. наз. непрерывной, дифференцируемой и т. п. (в точке или в области), если такими являются все функции r_j(t). Для функции r(t) одного переменного справедливы формулы:

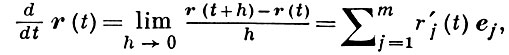
(формула Тейлора).

Множество концов векторов r(t), отложенных от нулевой точки пространства V, наз. годографом В.-ф. Первая производная ṙ(t) В.-ф. одного действительного переменного представляет собой вектор пространства V, касательный к годографу В.-ф. r(t) в точке r(t). Если r(t) есть закон движения материальной точки (t - время), то ṙ(t) является вектором мгновенной скорости точки в момент t. Вторая производная r̈(t) -вектор ускорения точки.

Аналогично формулам (2), (3) определяются частные производные и кратные интегралы В.-ф. нескольких переменных. О понятиях векторного анализа для В.-ф. см. Векторный анализ, Градиент, Дивергенция, Вихрь.

В бесконечномерном векторном пространстве, имеющем базис, представление В.-ф. вида (1) является бесконечным рядом и покоординатное определение операций математического анализа встречает трудности, связанные с понятиями сходимости рядов, возможности почленного дифференцирования и интегрирования и т. п.

Лит.: [1] Кочин Н. Е., Векторное исчисление и начала тензорного исчисления, 9 изд., М., 1965; [2] Рашевский П. К., Курс дифференциальной геометрии, 4 изд., М., 1956.

Л. П. Купцов.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.