ВЕКТОР-ФУНКЦИЙ АЛГЕБРА

ВЕКТОР-ФУНКЦИЙ АЛГЕБРА - произвольное семейство А функций x = {x(t)} на топологич. пространстве Т, принимающих в каждой точке t ∈ T значения в нек-рой алгебре A(t) (вообще говоря, зависящей от t), образующее алгебру относительно поточечных операций. Если каждая из алгебр A(t) является банаховой алгеброй, то А наз. В.-ф. а. при условии, что для любой функции x={x{t)} ∈ A функция t → ||x(t)|| непрерывна на Т. Важнейшие общие вопросы теории В.-ф. а.: описание идеалов в A в терминах идеалов в алгебрах A(t) и установление критерия принадлежности функции x = {x{t)} алгебре А; чаще всего рассматривается случай, когда А - банахова алгебра относительно нормы

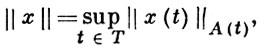
а Т - локально компактное или паракомпактное пространство. Особый интерес представляет В.-ф. а., связанная с семейством С*-алгебр A (t); в этом частном случае известны некоммутативные аналоги Вейерштрасса-Стоуна теоремы и нек-рые теоремы о реализации С*-алгебр (в частности, С*-алгебр с непрерывным следом) в виде В.-ф. а. В свою очередь, эти теоремы позволяют в нек-рых случаях доказать коммутативность совокупности операторов, перестановочных с операторами симметричных представлений алгебр с инволюцией (континуальный аналог леммы Шура).

А. И. Штерн.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.