
ВЕКТОРНЫЙ АНАЛИЗ
ВЕКТОРНЫЙ АНАЛИЗ - раздел векторного исчисления, в к-ром изучаются векторные поля и скалярные поля.
Одним из основных понятий В. а. для изучения скалярных полей является градиент. Скалярное поле u(М) наз. дифференцируемым в точке М области D, если приращение поля Δu в точке М может быть представлено в виде:
Δu = f(Δr) + о(ρ),
где Δr - вектор, соединяющий точку М с М', ρ = ρ(M, М') - расстояние между точками М и М', а f(Δr)-линейная форма относительно вектора Δr. Линейная форма f(Δr) единственным образом может быть представлена в следующем виде:
f(Δr) = (g, Δr),
где g - не зависящий от Δr (т. е. выбора точки М') вектор. Вектор g наз. градиентом скалярного поля и обозначается символом grad u. В случае, когда скалярное поле дифференцируемо в каждой точке нек-рой области, grad u является векторным полем. Градиент всегда направлен ортогонально линии (поверхности) уровня u(М) = const скалярного поля и с производной по направлению e связан соотношением:
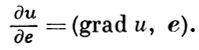
Для изучения векторных полей используется понятие дивергенции и ротора. Пусть векторное поле a(М) наз. дифференцируемым в точке М нек-рой области D, т. е. приращение поля Δa в точке М единственным образом может быть представлено в виде:
Δa = АΔr + о(|Δr|),
где Δr = |MM'|, А - линейный оператор, не зависящий от Δr (от выбора точки М'). Дивергенцией div a векторного поля a(М) наз. следующий скалярный инвариант линейного оператора А:
div a ≡ (ri, Ari), (*)
где r'i, ri - взаимные базисы (ri, rk) = δki (δki - символ Кронекера). Если a(M)-поле скоростей в установившемся потоке несжимаемой жидкости, то div a в точке М означает интенсивность источника (div a > 0) или стока (div a < 0), находящихся в точке М, или отсутствие их (div a = 0).
Вихрем (ротором) rot a векторного поля a(M) наз. следующий векторный инвариант линейного оператора А из (*):
rot a = [ri, Аri],
где ri, ri, - взаимные базисы. Вихрь векторного поля может быть интерпретирован как векторная «вращательная составляющая» этого поля.
Для векторных и скалярных полей класса С2 возможны повторные операции, напр.:
rot grad u = 0, div rot a = 0, rot rot a = grad div a - Δa, div grad u = Δu,
где Δ - оператор Лапласа.
Градиент, дивергенция и вихрь обычно наз. основными дифференциальными операциями В. а. О свойствах основных дифференциальных операций В. а. и записи в специальных системах координат см. Вихрь, Градиент, Дивергенция.
В терминах основных операций В. а. могут быть записаны основные интегральные формулы, связывающие объемные, поверхностные и контурные интегралы. Пусть векторное поле непрерывно дифференцируемо в конечной связной области V, граница L - кусочно гладкая.
Пусть S - ограниченная, полная, кусочно гладкая двусторонняя поверхность с кусочно гладкой границей ∂S. Тогда справедлива Стокса формула:
∬S(n, rot a) ds = ∮∂S(a, t) dl,
причем нормальный к S вектор n и касательный к ∂S вектор t должны определять согласованные ориентации поверхности S и края ∂S. Интеграл ∮∂S(a, t) dl наз. циркуляцией векторного поля a по кривой ∂S. Если циркуляция векторного поля по любой замкнутой кусочно гладкой кривой, расположенной в нек-рой области, равна нулю, то векторное поле наз. потенциальными этой области. В односвязной области векторное поле потенциальное, если rot a = 0. Для потенциального векторного поля существует так наз. скалярный потенциал - функция v(M) такая, что a = grad v; при этом
∫A͝B(a, t) dl = v(B) - v(A),
где точки A, B ∈ D, АВ - кусочно гладкая кривая, t - единичный вектор касательной к АВ, dl - дифференциал дуги.
Пусть векторное поле a(М) непрерывно и дифференцируемо в конечной связной области V с кусочно гладкой границей ∂V, тогда справедлива Остроградского формула:
∭V div a dσ = ∬∂V (n, a) ds,
где n - вектор внешней нормали к ∂V.
Интеграл ∬∂V (n, a) ds наз. потоком векторного поля a(М) через поверхность ∂V. Если поток векторного поля через любую замкнутую кусочно гладкую несамопересекающуюся ориентированную поверхность, расположенную в V и представляющую собой границу нек-рой ограниченной подобласти области V, равен нулю, то векторное поле a(М) наз. соленоидальным в области V. Для того чтобы непрерывно дифференцируемое векторное поле было соленоидальным, необходимо и достаточно, чтобы div a = 0 во всех точках V. Для соленоидального векторного поля a(М) существует так наз. векторный потенциал -функция A (M) такая, что
a = rot А (М).
Если дивергенция и вихрь векторного поля определены в каждой точке М области D, то всюду в D векторное поле может быть представлено в виде суммы потенциального a1(М) и соленоидального a2(М) полей (теорема Гельмгольца):
a(M) = a1(М) + a2(M).
Векторные поля, для к-рых div a = 0, rot a = 0, наз. гармоническими. Потенциал и гармонич. поля удовлетворяет уравнению Лапласа. Скалярное поле v также наз. гармоническим.
Лит. см. при статье Векторное исчисление.
А. Б. Иванов.
Источники:
- Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'