ВЕКТОРНОЕ РАССЛОЕНИЕ

ВЕКТОРНОЕ РАССЛОЕНИЕ - локально тривиальное расслоение π : X → B, каждый слой к-рого π^-1(b) наделен структурой (конечномерного) векторного пространства V над телом 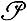; dim V наз. размерностью В. р. Сечения В. р. π образуют локально свободный модуль Г(π) над кольцом непрерывных функций на В со значениями в 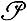. Морфизмом В. р. наз. морфизм расслоений f : π → π', для к-рого каждое отображение является линейным отображением. Совокупность В. р. и их морфизмов образует категорию Bund. Понятие В. р. возникло как обобщение касательного расслоения и нормального расслоения в дифференциальной геометрии; в настоящее время оно является базой и орудием исследования в различных областях математики - в дифференциальной и алгебраич. топологии, теории линейных связностей, алгебраич. геометрии, теории (псевдо)дифференциальных операторов и т. д.

Подмножество X' ⊂ X такое, что π|_X, : X' → B есть В. р. и X' ∩ π^-1(b) - векторное подпространство π^-1(b), наз. подрасслоением В. р. л. Пусть, напр., V - векторное пространство и G_k(V) - Грассмана многообразие подпространства V размерности k; тогда подпространство произведения G_k(V) × V, состоящее из пар (р, v) таких, что v ∈ p, есть подрасслоение γ_k тривиального В. p. G_k(V) × V; объединение всех векторных пространств π^-1(b)/π^-1₂~1(b), где π₂ - подрасслоение π, снабженное фактортопологией, наз. фактор-расслоением В. р. л. Пусть, далее, V - векторное пространство и G^k(V) - комногообразие Грассмана подпространств V коразмерности k; тогда факторпространство произведения G^k(V) × V по подрасслоению, состоящему из пар (р, v) с v ∈ p, есть факторрасслоение γ^k тривиального В. p. G^k(V) × V. Понятия подрасслоения и факторрасслоения используются в конструкциях стягивания и склеивания, применяющихся для построения В. р. над факторпространствами.

B-морфизм В. р. f : π → π' наз. точным, если dim kеrf|π^-1(b) локально постоянна на B. Инъективный и сюръективный морфизмы являются точными и наз. соответственно мономорфизмом и эпиморфизмом В. р. Для точного морфизма f однозначно определены следующие В. р.: Kеr f (ядро f) - подрасслоение π, Im f (образ f) - подрасслоение π', Соkеr f (коядро f) - факторрасслоение π, Coim f (кообраз f) - факторрасслоение π'; каждое подрасслоение π₁ является образом нек-рого мономорфизма i : π₁ → π, а факторрасслоение π₂ - коядром нек-рого эпиморфизма j : π → π₂. Последовательность B-морфизмов В. р.

... → π' → π → π'' → ...

наз. точной, если для всех b ∈ В является точной последовательность

... → (π')^-1 (b) → π^-1(b) → (π'')^-1(b) → ...

В частности, последовательность

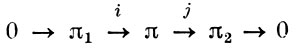
(где 0 - нулевое В. p.: Х = В, π = id) точна, если i -мономорфизм, j - эпиморфизм и Im i = Кеr j. Совокупность В. р. над В и их точных B-морфизмов образует точную подкатегорию Вund_B категории Bund.

Для любого В. р. π : X → B и отображения и : В₁ → В -индуцированное расслоение u*(π) снабжается такой структурой В. р., что морфизм U : u*(π) → π является морфизмом В. р. Эта структура единственна и обладает тем свойством, что каждое отображение (u*(π))^-1(b) → π^-1(u(b)) является изоморфизмом векторных пространств. Напр., каждое В. р. размерности k над пара-компактным пространством В изоморфно В. р. u*(γ_k) и ũ*(γ^k), индуцированным нек-рыми отображениями и : B → G_k(V) и ũ : B → G^k(V) соответственно, причем гомотопные отображения индуцируют изоморфные В. р., и, если dim V ≠ ∞, - наоборот: изоморфным В. р. соответствуют гомотопные отображения u и ũ. Это -одна из основных теорем гомотопической классификации В. р., выражающая универсальность В. p. γ_k и γ^k по отношению к классифицирующим отображениям u и ũ.

Любой непрерывной операции (функтору) Т на категории векторных пространств однозначно соответствует непрерывный функтор на категории В. р. над В; таким образом строятся расслоения, ассоциированные с данным В. р.: тензорные расслоения, В. р. морфизмов Ноm_B (π, π') и, в частности, сопряженное В. р. π*, внешние степени В. р. и т. д., сечения к-рых наделяют В. р. дополнительными структурами, широко используемыми в приложениях.

Для В. р. π и π' определяются прямая сумма (сумма Уитни) π ⊕ π' и тензорное произведение π ⊗ π', -относительно этих операций множество классов Vekt_B, изоморфных над В, В. р. образуют полукольцо, играющее важную роль в построении К-функтора; так, если для В. р. π и π' существуют тривиальные В. р. θ и θ' такие, что В. р. π ⊕ θ и π' ⊕ θ' изоморфны (т. е. π и π' стабильно эквивалентны), то их образы в пополнении К(В) полукольца Vekt_B совпадают, при этом существование обратного В. р. для любого В. р. над паракомпактным пространством влечет совпадение кольца К(В) и множества классов стабильной эквивалентности В. р.

Для каждого В. р. π : Х → В над паракомпактным пространством В существует сечение β В. р.

π* ⊕ π* = Ноm (π ⊕ π, Р),

где Р - тривиальное одномерное В. р., являющееся на каждом слое π^-1(b) положительно определенной формой, т. е. π - метризуемое; это позволяет установить, в частности, расщепляемость любой точной последовательности В. р. 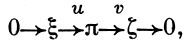, в которой π метризовано,- существование такого морфизма w : ξ ⊕ ζ → π, что wi = u, vw = j, причем i - вложение в первое слагаемое, j - проекция на второе слагаемое.

Отождествлением в каждом слое π^-1(b) В. р. π : X → B точек, лежащих на одной прямой, проходящей через 0, получается расслоение π₀ : П_(π) → B, ассоциированное с В. р. π и наз. его проективизацией; слоем π₀ является проективное пространство П(V), ассоциированное с V. С помощью этого расслоения изучаются Тома пространства Т'(π) = П(π ⊕ θ)/П(π), используемые для гомотопической интерпретации классов бордантных многообразий, характеристических классов В. р., описывающих гомологические свойства многообразий, и т. д.

Понятие В. р. обобщается на случай, когда слой является бесконечномерным векторным пространством; при этом следует различать разные топологии пространства морфизмов Ноm(π, π'), вносить соответствующие изменения в определение точности морфизмов и их последовательностей, а также в построение В. р., ассоциированных с непрерывными функторами на категории бесконечномерных векторных пространств.

Лит.: [1] Годбийон К., Дифференциальная геометрия и аналитическая механика, пер. с франц., М., 1973; [2] Атья М., Лекции по K-теории, пер. с англ., М., 1967; [3] Ленг С., Введение в теорию дифференцируемых многообразий, пер. с англ., М., 1967; [4] Хьюзмоллер Д., Расслоенные пространства, пер. с англ., М., 1970; [5] Чжэнь Шэн-шэнь, Комплексные многообразия, пер. с англ., М., 1961; [6] Xирцебрух Ф., Топологические методы в алгебраической геометрии, пер. с англ., М., 1973.

А. Ф. Щекутьев.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.