
ВЕКТОРНОЕ ПРОСТРАНСТВО
ВЕКТОРНОЕ ПРОСТРАНСТВО, линейное пространство, над полем K, - аддитивно записанная абелева группа Е, в которой определено умножение элементов на скаляры, т. е. отображение
К × Е → Е: (λ, х) → λх,
удовлетворяющее следующим аксиомам (х, y ∈ Е, λ, μ, 1 ∈ K):
1) λ(х + у) = λх + λу,
2) (λ + μ)x = λx + μx,
3) (λμ)x = λ(μx),
4) 1 ⋅ x = х.
Из аксиом 1)-4) вытекают следующие важные свойства векторного пространства (0 ∈ Е):
5) λ ⋅ 0 = 0,
6) 0 ⋅ х = 0,
7) (-1)x = -x.
Элементы В. п. наз. точками В. п., или векторами, а элементы поля K - скалярами.
Наибольшее применение в математике и приложениях имеют В. п. над полем ℂ комплексных чисел или над полем ℝ действительных чисел; они наз. соответственно комплексными В. п. или действительными В. п.
Аксиомы В. п. выявляют нек-рые алгебраич. свойства многих классов функций, часто встречающихся в анализе. Из примеров В. п. самыми фундаментальными и наиболее ранними являются n-мерные евклидовы пространства. Почти столь же важными примерами являются многие функциональные пространства: пространство непрерывных функций, пространство измеримых функций, пространство суммируемых функций, пространство аналитич. функций, пространство функций ограниченной вариации.
Понятие В. п. есть частный случай понятия модуля над кольцом, а именно, В. п. есть унитарный модуль над полем. Унитарный модуль над некоммутативным телом также наз. векторным пространством над телом; теория таких В. п. во многом сложнее теории В. п. над полем.
Одной из важных задач, связанных с В. п., является изучение геометрии В. п., т. е. изучение прямых в В. п., плоских и выпуклых множеств в В. п., подпространств В. п. и базисов в В. п.
Векторным подпространством, или просто подпространством, В. п. Е над полем К наз. подмножество F ⊂ E, замкнутое относительно действий сложения и умножения на скаляр. Подпространство, рассматриваемое отдельно от вмещающего его пространства, есть В. п. над тем же полем.
Прямой линией, проходящей через две точки х и y В. п. Е, наз. множество элементов z ∈ E вида z = λx + (1 - λ)y, λ ∈ K. Множество G ∈ E наз. плоским множеством, если вместе с любыми двумя точками оно содержит прямую, проходящую через эти точки. Каждое плоское множество получается из нек-рого подпространства с помощью сдвига (параллельного переноса): G = x + F; это означает, что каждый элемент z ∈ G представим единственным образом в виде z = x + y, y ∈ F, причем это равенство осуществляет взаимно однозначное соответствие между F и G.
Совокупность всех сдвигов Fx = x + F данного подпространства F образует В. п. над K, наз. фактор-пространством E/F, если определить операции следующим образом:
FxFy = Fx+y; λFx = Fλx, λ ∈ К.
Пусть М = {хα}α∈A- произвольное множество векторов из Е; линейной комбинацией векторов хα ∈ Е наз. вектор х, определенный формулой
х = ∑αλαxα, λα ∈ K,
в к-рой лишь конечное число коэффициентов отлично от нуля. Совокупность всех линейных комбинаций векторов данного множества М является наименьшим подпространством, содержащим М, и наз. линейной оболочкой множества М. Линейная комбинация наз. тривиальной, если все коэффициенты λα равны нулю. Множество М наз. линейно независимым множеством, если все нетривиальные линейные комбинации векторов из М отличны от нуля.
Любое линейно независимое множество содержится в нек-ром максимальном линейно независимом множестве М0, т. е. в таком множестве, к-рое перестает быть линейно независимым после присоединения к нему любого элемента из Е.
Каждый элемент х ∈ Е может быть единственным образом представлен в виде линейной комбинации элементов максимального линейно независимого множества:
х = ∑αλαxα, xα ∈ M0.
В связи с этим максимальное линейно независимое множество наз. базисом В. п. (алгебраическим базисом). Все базисы данного В. п. имеют одинаковую мощность, к-рая наз. размерностью В. п. Если эта мощность конечна, пространство наз. конечномерным В. п.; в противном случае оно наз. бесконечномерным В. п.
Поле K можно рассматривать как одномерное В. п. над полем K; базис этого В. п. состоит из одного элемента; им может быть любой элемент, отличный от нуля. Конечномерное В. п. с базисом из n элементов наз. n-мерным пространством.
В теории действительных и комплексных В. п. важную роль играет теория выпуклых множеств. Множество М в действительном В. п. наз. выпуклым множеством, если вместе с любыми двумя его точками х, у отрезок tx + (1 - t)y, t ∈ [0, 1], также принадлежит М.
Большое место в теории В. п. занимает теория линейных функционалов на В. п. n связанная с этим теория двойственности. Пусть Е есть В. п. над полем K. Линейным функционалом на Е наз. аддитивное и однородное отображение f : Е → К:
f(x + y) = f(x) + f(y), f(λx) = λf(x).
Множество Е* всех линейных функционалов на Е образует В. п. над полем K относительно операций
(f1 + f2)(x) = f1(x) + f2(x), (λf)(x) = λf(x), х ∈ Е, Х ∈ К, f1, f2, f ∈ Е*.
Это В. п. наз. сопряженным (или двойственным) пространством (к Е). С понятием сопряженного пространства связан ряд геометрич. терминов. Пусть D ⊂ E (соответственно Г ⊂ Е*); аннулятором множества D, или ортогональным дополнением множества D (соответственно множества Г) наз. множество
D⊥ = {f ∈ Е*: f(x) = 0 для всех х ∈ D}
(соответственно Г⊥ = {х ∈ Е : f(x) = 0 для всех f ∈ Г}); здесь D⊥ и Г⊥ - подпространства соответственно пространств Е* и Е. Если f - ненулевой элемент из Е*, то {f} есть максимальное собственное линейное подпространство в Е, наз. иногда гиперподпространством; сдвиг такого подпространства наз. гиперплоскостьюв Е; всякая гиперплоскость имеет вид
{x : f(x) = λ), где f ≠ 0, f ∈ Е*, λ ∈ K.
Если F - подпространство В. п. Е, то существуют естественные изоморфизмы между F* и
E*/F⊥ и между (E/F)* и F⊥.
Подмножество Г ⊂ E* наз. тотальным подмножеством над Е, если его аннулятор содержит лишь нулевой элемент: Г⊥ = {0}.
Каждому линейно независимому множеству {хα}α∈A ⊂ E можно сопоставить сопряженное множество {fα}α∈A ⊂ E*, т.е. такое множество, что fα(xβ) = δαβ {Кронекера символ) для всех α, β ∈ A. Множество пap {хα, fα} наз. при этом биортогональной системой. Если множество {хα} есть базис в Е, то {fα} тотально над Е.
Значительное место в теории В. п. занимает теория линейных преобразований В. п. Пусть Е1, Е2 - два В. п. над одним и тем же полем К. Линейным отображением, или линейным оператором, Т, отображающим В. п. Е1 в В. п. Е2 (или линейным оператором из Е1 в Е2), наз. аддитивное и однородное отображение пространства Е1 в Е2:
Т(х + у) = Тх + Ту; Т(λх) = λТ(х); х, у ∈ Е1.
Частным случаем этого понятия является линейный функционал, или линейный оператор из Е1 в K. Линейным отображением является, напр., естественное отображение В. п. Е на факторпространство E/F, сопоставляющее каждому элементу х ∈ Е плоское множество Fx ∈ E/F. Совокупность ℒ(Е1, Е2) всех линейных операторов Т: Е1 →Е2 образует В. п. относительно операций
(Т1 + Т2)х = Т1х + Т2х; (λТ)х = λТх; х ∈ Е1; λ ∈ K; T1, T2, Т ∈ ℒ(Е1, Е2).
Два В. п. Е1 и Е2 наз. изоморфными В. п., если существует линейный оператор («изоморфизм»), осуществляющий взаимно однозначное соответствие между их элементами. Е1 и Е2 изоморфны тогда и только тогда, когда их базисы имеют одинаковую мощность.
Пусть Т - линейный оператор, отображающий Е1 в Е2. Сопряженным линейным оператором, или двойственным линейным оператором, по отношению к Т, наз. линейный оператор Т* из E*2 в Е*1, определенный равенством
(Т*φ)х = φ(Тх) для всех х ∈ Е1, φ ∈ Е*2.
Имеют место соотношения Т*-1(0) =[T(E1)]⊥, Т*(Е*2) = [Т-1(0)]⊥, откуда следует, что Т* является изоморфизмом тогда и только тогда, когда Т является изоморфизмом.
С теорией линейных отображений В. п. тесно связана теория билинейных отображений и полилинейных отображений В. п.
Важную группу задан теории В. п. образуют задачи продолжения линейных отображений. Пусть F - подпространство В. п. Е1, Е2 - линейное пространство над тем же полем, что и Е1, и пусть Т0 - линейное отображение F в Е2; требуется найти продолжение Т отображения T0, определенное на всем Е1 и являющееся линейным отображением Е1 в Е2. Такое продолжение всегда существует, но дополнительные ограничения на функции (связанные с дополнительными структурами в В. п., напр., топологией или отношением порядка) могут сделать задачу неразрешимой. Примерами решения задачи продолжения являются Хана-Банаха теорема и теоремы о продолжении положительных функционалов в пространствах с конусом.
Важным разделом теории В. п. является теория операций над В. п., т. е. способов построения новых В. п. по известным. Примеры таких операций - известные операции взятия подпространства и образования факторпространства по подпространству. Другие важные операции - построение прямой суммы, прямого произведения и тензорного произведения В. п.
Пусть {Еα}α∈I - семейство В. п. над полем К. Множество Е - произведение множеств Еα - можно превратить в В. п. над полем К, введя операции
(xα) + (yα) = (xα + yα); λ(xα) = (λxα); λ ∈ K; xα, yα ∈ Eα, α ∈ I;
полученное В. п. Е наз. прямым произведением В. п. Еα и обозначается Пα∈IЕα. Подпространство В. п. Е, состоящее из всех тех наборов (хα), для каждого из к-рых множество {α : хα ≠ 0} конечно, наз. прямой суммой В. п. Еα и обозначается ΣαEα или Σα + Eα; Для конечного числа слагаемых эти определения совпадают; в этом случае используются обозначения:
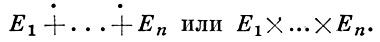
Пусть Е1, Е2 - два В. п. над полем K; Е'1, Е'2 -тотальные подпространства В. п. E*1, Е*2, и Е1 □ Е2 -В. п., имеющее своим базисом совокупность всех элементов пространства Е1 × Е2. Каждому элементу x □ y ∈ E1 □ E2 сопоставляется билинейная функция b = Т(х, у) на Е'1 × Е2 по формуле b(f, g) = f(x)g(y), f ∈ E'1, g ∈ E'2. Это отображение базисных векторов x □ y ∈ E1 □ E2 можно продолжить до линейного отображения Т В. п. Е1 □ Е2 в В. п. всех билинейных функционалов на Е'1 × Е'2. Пусть E0 = T-1(0). Тензорным произведением В. п. Е1 и Е2 наз. факторпространство Е1 ○ Е2= (E1 □ E2)/E0; образ элемента x □ y обозначается х ○ у. В. п. Е1 ○ Е2 изоморфно В. п. билинейных функционалов на Е1 × Е2 (см. Тензорное произведение векторных пространств).
Наиболее содержательной частью теории В. п. является теория конечномерных В. п. Но и понятие бесконечномерного В. п. часто оказывается плодотворным и имеет интересные приложения, особенно в теории топологических векторных пространств, т. е. В. п., наделенных топологией, определенным образом согласованной с его алгебраич. структурой.
Лит.: [1] Бурбаки Н., Алгебра. Алгебраические структуры. Линейная и полилинейная алгебра, пер. с франц., М., 1962; [2] Райков Д. А., Векторные пространства, М., 1962; [3] Дэй М. М., Нормированные линейные пространства, пер. с англ., М., 1961; , [4] Эдварде Р., Функциональный анализ, пер. с англ., М., 1969; [5] Халмош П., Конечномерные векторные пространства, пер. с англ., М., 1963; [6] Глазман И. М., Любич Ю. И., Конечномерный линейный анализ в задачах, М., 1969.
М. И. Кадец.
Источники:
- Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'