ВЕКТОРНОЕ ПОЛЕ

ВЕКТОРНОЕ ПОЛЕ на многообразии М-сечение касательного расслоения τ(М). Множество В. п. образует модуль над кольцом F дифференцируемых функций на М.

Пример 1. Для карты х_U многообразия М определяется i-е базисное В. п. 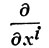по формуле

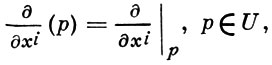
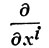 |_p есть i-й базисный касательный вектор к М в точке р, и любое В. п. однозначно представляется в виде

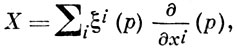
ξⁱ(р) наз. компонентами В. п. А в карте х_U. В. п. является дифференцированием кольца F, вследствие чего множество В. п. образует относительно операции коммутирования (скобки Ли) алгебру Ли.

Пример 2. Для карты х_U и f ∈ F функция X_f определяется формулой

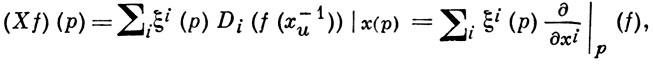
где D_i - частная производная по хⁱ, ξⁱ(р) = Ххⁱ(р); Xf наз. производной от f по направлению X.

Пример 3. Для карты х_U и f ∈ F коммутатор (скобка Ли) [X, Y] В. п.

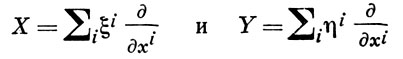
определяется формулой

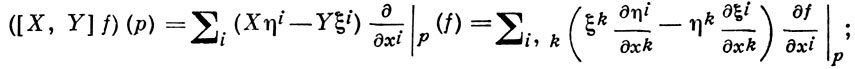
он удовлетворяет соотношениям:

[X, Y] = -[Y, X], [[X, Y], Z] + [[Y, Z], X]+[[Z, X], Y] = 0,

в частности

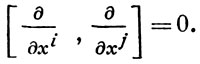
Каждое В. п. X индуцирует на М локальный поток-семейство диффеоморфизмов окрестности U

Ф : (-ε, +ε) × U → М

такое, что Ф (0, р) = р для р ∈ U и

Ф(t, р) = Ф_p(t): (-ε, ε) → М

- интегральный путь В. п. X, т. е.

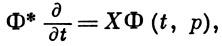
где Ф* ∂/∂t - В. п., касательное к отображению Ф_p(t). И наоборот, В. п. X ассоциировано с локальным потоком Ф(t, р) = Ф_t(р) - вариацией отображения Ф₀(р); при этом

Каждое В. п. определяет дифференцирование Ли LX тензорного поля типа λ со значениями в векторном пространстве (инфинитезимальное преобразование λ), соответствующее локальному потоку Ф(t, р), частными случаями к-рого являются действие В. п. на f ∈ F

L_Xf = Xf

и скобка Ли

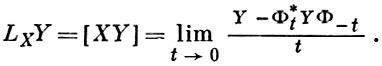
В. п. без особенностей порождает на М интегрируемую одномерную дифференциальную систему и ассоциированную с ней Пфаффа систему.

Обобщением понятия В. п. на многообразии является

B. п. вдоль отображения φ: N → M - сечение расслоения τ_φ(N), индуцированного φ, а также тензорное поле типа λ - сечение ассоциированного с τ(М) при помощи функтора λ расслоения λ[τ].

Лит.: [1] Годбийон К., Дифференциальная геометрия и аналитическая механика, пер. с франц., М., 1973; [2] Громол Д., Клингенберг В., Мейер В., Риманова геометрия в целом, пер. с нем., М., 1971; [3] Ленг С., Введение в теорию дифференцируемых многообразий, пер. с англ., М., 1967; [4] Номидзу К., Группы Ли и дифференциальная геометрия, пер. с англ., М., 1960; [5] Постников М. М., Введение в теорию Морса, М., 1971; [6] Хелгасон C., Дифференциальная геометрия и симметрические пространства, пер. с англ., М., 1964.

А. Ф. Щекутьев.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.