ВЕКТОРНОЕ АНАЛИТИЧЕСКОЕ РАССЛОЕНИЕ

ВЕКТОРНОЕ АНАЛИТИЧЕСКОЕ РАССЛОЕНИЕ - локально тривиальное аналитич. расслоение над аналитич. пространством, слои к-рого обладают структурой n-мерного векторного пространства над основным полем к (если k = ℂ - поле комплексных чисел, то аналитич. расслоение наз. также голоморфным). Число n наз. рангом, или размерностью, расслоения. Так же, как в топологич. случае (см. Векторное расслоение), определяются категория векторных аналитич. расслоений, понятия подрасслоения, факторрасслоения, прямой суммы, тензорного произведения, внешней степени В. а. р. и т. д.

Аналитич. сечения В. а. р. Е → X с базой X образуют модуль Г(Е) над алгеброй А(X) аналитич. функций на базе. В случае, когда k = ℂ и X компактно, Г(E) -конечномерное векторное пространство над ℂ (см. Конечности теоремы). Если же X - конечномерное комплексное пространство Штейна, то Г(Е) - проективный модуль конечного типа над А(X), причем соответствие Е ↦ Г(Е) определяет эквивалентность категории В. а. р. над X и категории проективных А(X)-модулей конечного типа [4].

Примерами В. а. р. являются касательное расслоение на аналитич. многообразии X (его аналитич. сечения - аналитич. векторные поля на X), нормальное расслоение на подмногообразии Y ⊂ X.

Классификация В. а. р. ранга n на заданном аналитич. пространстве X равносильна классификации главных аналитических расслоений с базой X и структурной группой GL(n, k) и при n > 1 проведена полностью только в некоторых специальных случаях. Для проективных комплексных алгебраич. многообразий X она совпадает с классификацией алгебраич. векторных расслоений (см. Сравнения теоремы в алгебраической геометрии) .

В. а. р. ранга 1 на комплексном пространстве X (иначе, расслоения на комплексные прямые или линейные расслоения) играют важную роль в комплексной аналитич. геометрии. Каждый дивизор на пространстве X естественным образом определяет аналитич. расслоение ранга 1, причем два дивизора определяют изоморфные расслоения тогда n только тогда, когда они линейно эквивалентны. На проективном алгебраич. многообразии всякое линейное аналитич. расслоение определяется дивизором. Вложимость комплексного пространства X в проективное пространство тесно связана с существованием на X обильных линейных расслоений (см. Обильное векторное расслоение). Если на комплексном пространстве X задана дискретная группа Г его автоморфизмов, то каждый фактор автоморфности группы Г определяет линейное расслоение над X/Г, аналитич. сечения к-рого суть соответствующие автоморфные формы. В. а. р. ранга 1 составляют группу H¹(X, 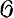^*_X), где 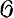^*_X - пучок обратимых элементов структурного пучка. Сопоставление каждому расслоению его 1-го класса Чжэня дает гомоморфизм

γ : H¹(X, 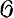^*_X) → H²(X, ℤ),

ядро к-рого есть множество топологически тривиальных линейных расслоений. В случае, когда X - комплексное многообразие, Im γ можно описать как множество классов когомологий, представимых замкнутыми дифференциальными формами типа (1,1). Если X, кроме того, компактно и кэлерово, то Кеr γ изоморфно Пикара многообразию многообразия X и тем самым является комплексным тором [2].

Каждому В. а. p. V ранга n на аналитич. пространстве X соответствует пучок ростков аналитич. сечений расслоения V, к-рый является локально свободным аналитическим пучком ранга n на X. Это соответствие определяет эквивалентность между категориями В. а. р. и локально свободных аналитич. пучков на X. Попытка обобщить этот результат на произвольные когерентные аналитич. пучки привела к следующему обобщению понятия В. а. р. [3]. Сюръективный морфизм π : V → X наз. аналитическим семейством векторных пространств над X (или линейным пространством над X), если его слои обладают структурой конечномерных векторных пространств над k, причем операции сложения, умножения на скаляр и нулевое сечение удовлетворяют естественным требованиям аналитичности. Если k = ℂ (или k = ℝ и X когерентно), то аналитич. семейство векторных пространств π : V → X определяет когерентный аналитич. пучок F на X: для U ⊂ X группа F(U) есть пространство аналитич. функций на π^-1(U), линейных на слоях. Тем самым определяется двойственность между категориями аналитич. семейств векторных пространств и когерентных аналитич. пучков на X.

Лит.: [1] Ганнинг Р., Росси X., Аналитические функции многих комплексных переменных, пер. с англ., М., 1969; [2] Чжэнь Шэн-шэнь, Комплексные многообразия, пер. с англ., М., 1961; [3] Fischer G., «Arch. Math.», 1967, Bd 18, s. 609-17; [4] Forster O., Ramspott K. J., там же, 1968, Bd 19, s. 417-22.

А. Л. Онищик.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.