ВЕКТОРНАЯ ТРУБКА

ВЕКТОРНАЯ ТРУБКА - замкнутое множество Ф точек области Ω пространства, в к-рой задано векторное поле a(М), такое, что всюду на его граничной поверхности S вектор нормали n ортогонален a. В. т. Ф состоит из векторных линий Г поля a, т. е. кривых в Ω, в каждой точке к-рых направление касательной совпадает с направлением a. Линия Г целиком содержится в Ф, если одна точка Г содержится в Ф. Если a - поле скоростей стационарного потока жидкости, то Г - траектория частицы жидкости, а Ф -часть Ω, к-рую при движении «заметает» фиксированное множество частиц жидкости.

Интенсивностью I трубки Ф в сечении S наз. поток (см. Векторный анализ) поля a через S':

I(S') = ∬S' (a, n) dσ,

где n - единичный вектор нормали к S'. Если поле a - соленоидально (div a = 0), то выполняется закон сохранения интенсивности В. т.:

I(S') = I(S'').

Пусть а₁(х, у, z), а₂(х, у, z), а₃(х, у, z) - декартовы прямоугольные координаты вектора a = a(М); х, у, z -координаты точки М. Тогда локально граница Ф задается уравнением F(x, у, z) = const, где F(x, у, z) удовлетворяет уравнению с частными производными:

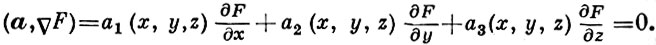
Ю. П. Пытьев.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.