ВЕКТОРНАЯ АЛГЕБРА

ВЕКТОРНАЯ АЛГЕБРА - раздел векторного исчисления, в к-ром изучаются простейшие операции над (свободными) векторами. К числу этих операций относятся линейные операции над векторами: операция сложения векторов и умножения вектора на число.

Суммой a+b векторов a и b наз. вектор, проведенный из начала a к концу b, если конец a и начало a совмещены. Операция сложения векторов обладает свойствами:

a + b = b + a (коммутативность), (a + b) + c = a + (b + c) (ассоциативность), a + 0 = a (наличие нулевого элемента), a + (-a) = 0 (наличие противоположного элемента),

где 0 - нулевой вектор, -a есть вектор, противоположный вектору a. Разностью a - b векторов a и b наз. вектор x такой, что x + b = a.

Произведением λa вектора a на число λ в случае λ ≠ 0, a ≠ 0 наз. вектор, модуль к-рого равен |λ||a| и к-рый направлен в ту же сторону, что и вектор a, если λ > 0, и в противоположную, если λ < 0. Если λ = 0 или (и) a = 0, то λa = 0. Операция умножения вектора на число обладает свойствами:

λ(a + b) = λa + λb (дистрибутивность относительно сложения векторов),

(λ + μ)a = λa + μa (дистрибутивность относительно сложения чисел),

λ(μa) = (λμ)a (ассоциативность),

1⋅a = a (умножение на единицу).

Множество всех векторов пространства с введенными в нем операциями сложения и умножения на число образует векторное пространство (линейное пространство).

В В. а. важное значение имеет понятие линейной зависимости векторов. Векторы a, b, ..., c наз. линейно зависимыми векторами, если существуют числа α, β, ..., γ, из к-рых хотя бы одно отлично от нуля, такие, что справедливо равенство

αa + βb + ... + γc = 0. (1)

Для линейной зависимости двух векторов необходима и достаточна их коллинеарность, для линейной зависимости трех векторов необходима и достаточна их компланарность. Если один из векторов a, b, ..., c нулевой, то они линейно зависимы. Векторы а, Ь, ..., с наз. линейно независимыми, если из равенства (1) следует, что числа α, β, ..., ν равны нулю. На плоскости существует не более двух, а в трехмерном пространстве не более трех линейно независимых векторов.

Совокупность трех (двух) линейно независимых векторов e₁, e₂, e₃ трехмерного пространства (плоскости), взятых в определенном порядке, образует базис. Любой вектор а единственным образом представляется в виде суммы:

a = a₁e₁ + a₂e₂ + a₃e₃.

Числа a₁, a₂, a₃ наз. координатами (компонентами) вектора a в данном базисе и пишут a = {a₁, a₂, a₃}.

Два вектора a = {a₁, a₂, a₃} и b = {b₁, b₂, b₃} равны тогда и только тогда, когда равны их соответствующие координаты в одном и том же базисе. Необходимым и достаточным условием коллинеарности векторов a = {a₁, a₂, a₃} и b = {b₁, b₂, b₃}, b ≠ 0, является пропорциональность их соответствующих координат: a₁ = λb₁, a₂ = λb₂, a₃ = λb₃. Необходимым и достаточным условием компланарности трех векторовa = {a₁, a₂, a₃}, b = {b₁, b₂, b₃} и c = {c₁, c₂, c₃} является равенство

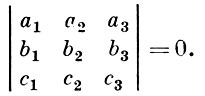
Линейные операции над векторами сводятся к линейным операциям над координатами. Координаты суммы векторов a = {a₁, a₂, a₃} и b = {b₁, b₂, b₃} равны суммам соответствующих координат: a + b = {a₁ + b₁, a₂ + b₂, a₃ + b₃}. Координаты произведения вектора a на число λ равны произведениям координат a на λ: λa = {λa₁, λa₂, λa₃}.

Скалярным произведением (a, b) ненулевых векторов a и b наз. произведение их модулей на косинус угла φ между ними:

(a, b) = |а||b| cos φ.

За φ принимается угол между векторами, не превосходящий я. Если a = 0 или b = 0, то скалярное произведение полагают равным нулю. Скалярное произведение обладает свойствами:

(a, b) = (b, a) (коммутативность),

(a, b+c)= (a, b) + (a, c) (дистрибутивность относительно сложения векторов),

λ(a, b) = (λa, b) = {a, λb) (сочетательность относительно умножения на число),

(a, b) = 0, лишь если a = 0 или (и) b = 0 или a⊥b.

Для вычисления скалярных произведений векторов часто пользуются декартовыми прямоугольными координатами, т. е. координатами векторов в базисе, состоящем из единичных взаимно перпендикулярных векторов (ортов) i, j, k(ортонормированный базис). Скалярное произведение векторов

a = {a₁, a₂, a₃} и b = {b₁, b₂, b₃},

заданных в ортонормированием базисе, вычисляется по формуле:

(a, b) = a₁b₁ + a₂b₂ + a₃b₃.

Косинус угла φ между ненулевыми векторами a = {a₁, a₂, a₃} и b = {b₁, b₂, b₃} может быть вычислен по формуле

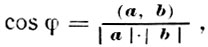
где .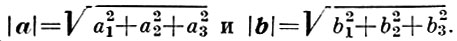

Косинусы углов вектора a = {a₁, a₂, a₃} с векторами базиса i, j, k наз. направляющими косинусами вектора a:

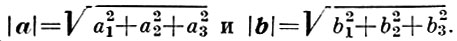
Направляющие косинусы обладают следующим свойством:

cos² α + cos² β + cos² γ = 1.

Осью наз. прямая с лежащим на ней единичным вектором e - ортом, задающим положительное направление на прямой. Проекцией Пр._ea вектора a на ось наз. направленный отрезок на оси, алгебраич. значение к-рого равно скалярному произведению вектора a на вектор e. Проекции обладают свойствами:

Пр._e (a + b) = Пр._ea + Пр._eb (аддитивность), λПр._ea = Пр._e λa (однородность).

Каждая координата вектора в ортонормированием базисе равна проекции этого вектора на ось, определяемую соответствующим вектором базиса.

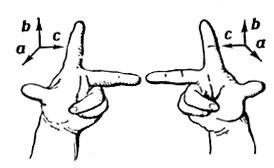
В пространстве различают правые и левые тройки векторов. Тройка некомпланарных векторов a, b, c наз. правой, если наблюдателю из их общего начала обход концов векторов a, b, c в указанном порядке кажется совершающимся по часовой стрелке. В противном случае a, b, c - левая тройка. Правая (левая) тройка векторов располагается так, как могут быть расположены соответственно большой, несогнутый указательный и средний пальцы правой (левой) руки (см. рис.). Все правые (или левые) тройки векторов наз. одинаково ориентированными. Ниже тройка векторов базиса i, j, k считается правой.

Пусть на плоскости задано направление положительного вращения (от i к j). Псевдоскалярным произведением a ∨ b ненулевых векторов a, и b наз. произведение их модулей на синус угла φ положительного вращения от a к b:

a ∨ b = |a||a| sin φ.

Псевдоскалярное произведение нулевых векторов полагают равным нулю. Псевдоскалярное произведение обладает свойствами:

a ∨ b = -b ∨ a (антикоммутативность),

a ∨ (b + c) = a ∨ b + a ∨ c (дистрибутивность относительно сложения векторов),

λ(a ∨ b) = λa ∨ b (сочетательность относительно умножения на число),

a ∨ b = 0, лишь если a = 0 или (и) b = 0 или a и b коллинеарны.

Если в ортонормированном базисе векторы a и b имеют координаты {a₁, а₂} и {b₁, b₂}, то

a ∨ b = a₁b₂ - а₂b₁.

Векторным произведением [a, b] ненулевых и неколлинеарных векторов a и b наз. вектор, модуль к-рого равен произведению их модулей на синус угла φ между ними, перпендикулярный a и b и направленный так, что тройка векторов a, b, [a, b] -правая:

[a, b] = |a||b| sin φ.

Векторное произведение полагают равным нулю, если a = 0 или (и) b = 0 или они коллинеарны. Векторное произведение обладает свойствами:

[a, b] = -[b, a] (антикоммутативность),

[a, b + c] = [a, b]+[a, c] (дистрибутивность относительно сложения векторов),

λ[a, b] = [λa, b] = [a, λb] (сочетательность относительно умножения на число),

[a, b] = 0, лишь если a = 0 или(и) b = 0 или a и b коллинеарны.

Если в ортонормированном базисе векторы a и b имеют координаты {a₁, а₂, а₃) и {b₁, b₂, b₃}, то

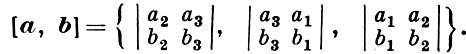
Смешанным произведением (a, b, c) векторов a, b, c наз. скалярное произведение вектора a на векторное произведение векторов b и c:

(a, b, c) = (a, [b, c]).

Смешанное произведение обладает свойствами:

(a, b, c) = (b, c, a) = (c, a, b) = -(c, a, c) = = -(c, b, a) = -(a, c, b).

(a, b, c) = 0, лишь если a = 0 или (и) b = 0 или (и) c = 0, или векторы a, b, c компланарны.

(a, b, c) > 0, если тройка векторов a, b, c - правая, (a, b, c) < 0, если a, b, c - тройка левая.

Модуль смешанного произведения равен объему параллелепипеда, построенного на векторах a, b, c. Если в ортонормированном базисе векторы a, b, c имеют координаты {a₁, а₂, а₃}, {b₁, b₂, b₃} и {c₁, c₂, c₃}, то

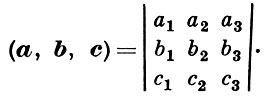
Двойным векторным произведением [a, b, c] векторов a, b, c наз. векторное произведение [a, [b, c]].

При вычислении двойного векторного произведения имеют место формулы:

[a, b, c] = [b, (a, c)] - [c, (a, b)], ([a, b], [c, d]) = (a, c) (b, d) - (a, d)(b, c), [[a, b], [c, d]] = (a, c, d)b - (b, c, d)a = (a, b, d)c - (a, b, c)d.

Лит.: [1] Александров П. С., Лекции по аналитической геометрии..., М., 1968; [2] Ефимов Н. В., Краткий курс аналитической геометрии, 9 изд., М., 1967; [3] Ильин В. А., Позняк Э. Г., Аналитическая геометрия, М., 1968; [4] Погорелов А. В., Аналитическая геометрия, 3 изд., М., 1968.

Ю. П. Пытьев.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.