ВЕЙНГАРТЕНА ДЕРИВАЦИОННЫЕ ФОРМУЛЫ

ВЕЙНГАРТЕНА ДЕРИВАЦИОННЫЕ ФОРМУЛЫ - формулы, дающие разложение производной единичного вектора нормали к поверхности по первым производным радиус-вектора этой поверхности. Если r = r(u, v) - радиус-вектор поверхности, n - единичный вектор нормали и Е, Р, G, L, М, N - коэффициенты соответственно первой и второй квадратичных форм поверхности, то В. д. ф. имеют вид

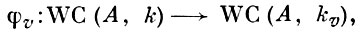
В. д. ф. установлены Ю. Вейнгартеном (J. Weingarten, 1861).

Лит.: [1]Рашевский П. К., Курс дифференциальной геометрии, 4 изд., М., 1956.

А. Б. Иванов.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.