ВЕЙЛЯ МЕТОД

ВЕЙЛЯ МЕТОД в теории чисел - метод для получения нетривиальных оценок тригонометрич. сумм вида

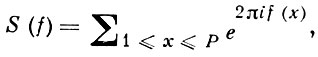
(1)

где

f(х) = α_nхⁿ + ... + α₁х,

а α_n, ..., α₁ - любые действительные числа. В. м. был разработан Г. Вейлем [1] для установления критериев равномерного распределения (см. Вейля критерий).

Сущность В. м. заключается в следующем. Сумма (1) возвышается в степень ρ₀ = 2^n-1 путем последовательных возвышений в квадрат с целью понижения степени многочлена f(x). Напр., на первом шаге

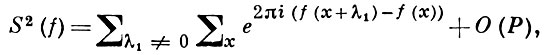
где суммирования производятся по интервалам длины 〈〈 P

f(x + λ₁) - f(х) = nα₁х^n-1 + ...

является многочленом степени n-1 относительно х (символы О(Р), 〈〈 Р обозначают величины порядка Р). На (n-1)-м шаге приходят к внутренней сумме

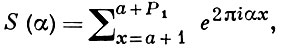
(2)

где Р₁ ≤ Р, α = n! λ₁, λ₂...λ_n-1α_n, λ_i ≠ 0. Суммы вида (2) оцениваются с помощью неравенства:

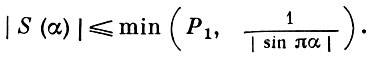
В результате получается оценка:

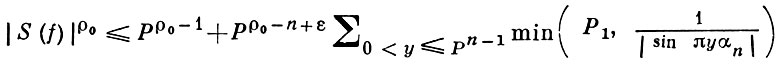
(3)

Из неравенства (3) выводятся различные оценки суммы (1) в случае, когда 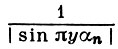будет величиной малой по сравнению с Р. Эти оценки зависят от точности, с к-рой коэффициент α_n многочлена f(x) аппроксимируется рациональными дробями.

Пример. Пусть

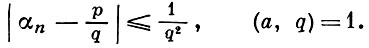
Тогда имеет место неравенство

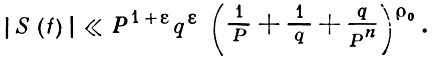
В частности, если

Р ≤ q ≤ Р^n-1,

то

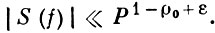
В. м. позволил решить в первом приближении ряд важных проблем теории чисел. С помощью оценки (3) и ее следствий было исследовано распределение дробных долей многочлена f(x). Решение Варинга проблемы, данное в 1919 Г. X. Харди (G. Н. Hardy) и Дж. И. Литлвудом (J. Е. Littlewood), опиралось на оценки сумм (1) с помощью В. м. При этом им удалось оценить значения r = r(k), для к-рых уравнение

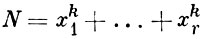
(N > 0 - целое, x_i - целые) разрешимо или даже имеет асимптотику для числа решений. Обобщение оценки (3) на случай функций f(х), не являющихся многочленами, но в известном смысле близких к ним, привело к улучшению нек-рых теорем в теории распределения простых чисел (оценка разности соседних простых чисел, оценка остаточного члена в асимптотич. формуле для числа π(N) простых чисел, не превосходящих N).

Недостаточная сила оценок, получаемых с помощью В. м., объясняется высокой степенью ρ₀, в к-рую возвышается сумма S(f). Нек-рое усовершенствование оценок сумм (1) дал И. ван дер Корпют (J. van der Corput). С помощью Виноградова метода получается весьма точная оценка сверху для интеграла

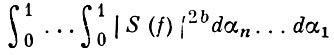
уже при b ≥ cn² (с > 0 - константа, n ὅ 2). Из этой оценки (см. Виноградова теорема о среднем) выводятся принципиально новые оценки сумм Вейля (1) (с понижающим множителем Р^-ρ, ρ = c₁n² ln n, c₁ > 0 - константа), недосягаемые для В. м.

Лит.: [1] Weyl Н., «Math. Аnn.», 1916, Bd 77, S. 313-52; [2] Виноградов И. М., Метод тригонометрических сумм в теории чисел, М., 1971.

Б. М. Бредихин.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.