ВЕЙЛЯ КОГОМОЛОГИИ

ВЕЙЛЯ КОГОМОЛОГИИ - когомологии алгебраич. многообразий с коэффициентами в поле нулевой характеристики, обладающие формальными свойствами, необходимыми для получения Лефшеца формулы для числа неподвижных точек. Необходимость такой теории была высказана А. Вейлем [1], показавшим, что рациональность дзета-функций многообразия и L-функций многообразия над конечным полем следует из формулы Лефшеца, а остальные гипотезы о ζ-функции естественно формулируются в когомологических терминах. Пусть многообразие X есть связная гладкая проективная схема над фиксированным алгебраически замкнутым полем k и пусть K - некоторое поле характеристики 0. Тогда когомологиями Вейля с полем коэффициентов K называется контравариантный функтор X → H*(X) из категории многообразий в категорию конечномерных градуированных антикоммутативных K-алгебр, удовлетворяющий следующим условиям:

1) Если n = dim X, то Н²ⁿ(Х) изоморфно К, и отображение

Нⁱ(Х) × H^2n-i(X) → Н²ⁿ(X),

определенное умножением в Н*(X), невырождено при всех i;

2) Н* (Х)⊗_KН*(Y) →̃ Н*(X × Y) (формула Кюннета);

3) Отображение циклов. Существует функториальный гомоморфизм γ_X группы С^p(Х) алгебраич. циклов X коразмерности р в Н^2p(Х), переводящий прямое произведение циклов в тензорное произведение, и нетривиальный в том смысле, что (для точки Р) γ_P превращается в канонич. вложение ℤ в K.

b_i(X) = dim_KHⁱ(X)

наз. i-м числом Бетти многообразия X.

Примеры. Если k = ℂ, то классические когомологий комплексных многообразий с коэффициентами в ℂ являются В. к. Если l - простое число, отличное от характеристики поля k, то этальные l-адические когомологий

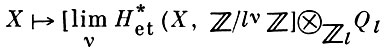
являются В. к. с коэффициентами в поле Q_l. Для В.к. верна формула Лефшеца

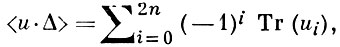
где 〈u⋅Δ〉 - индекс пересечения в X × X графика Г морфизма u с диагональю Δ ⊂ X × X, интерпретируемый также как число неподвижных точек эндоморфизма u, а Тr(u_i) - след эндоморфизма u_i, являющегося ограничением u на Нⁱ(X). Более того, эта формула верна также для соответствий, т. е. элементов u ∈ Н²ⁿ(X × X).

Лит.: [1] Weil A., «Bull. Amer. Math. Soc.», 1949, v. 55, p. 497-508; [2] Dix exposes sur la cohomologie des schemas, P., 1968, p. 359-86.

В. И. Данилов.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.