
ВЕЙЕРШТРАССА ЭЛЛИПТИЧЕСКИЕ ФУНКЦИИ
ВЕЙЕРШТРАССА ЭЛЛИПТИЧЕСКИЕ ФУНКЦИИ - функции, положенные К. Вейерштрассом в основу его общей теории эллиптических функций, излагавшейся им с 1862 на лекциях в Берлинском университете (см. [1], [2]). В отличие от более раннего построения теории эллиптич. функций, связанного с именами А. Лежандра (A. Legendre), Н. Абеля (N. Abel) и К. Якоби (С. Jacobi), в основу к-рого были положены эллиптич. функции 2-го порядка, имеющие в параллелограмме периодов два простых полюса, основная В. э. ф. имеет в параллелограмме периодов один полюс 2-го порядка. В теоретич. отношении теория Вейерштрасса более проста, так как исходная в этой теории функция ℘(z) и ее производная служат образующими алгебраич. поля эллиптич. функций с заданными примитивными периодами.
Пэ-функция (℘-функция) Вейерштрасса ℘(z) (℘ - знак Вейерштрасса, стилизованная буква «пэ») для заданных примитивных периодов 2ω1, 2ω3, Im (ω3/ω1) > 0, определяется рядом
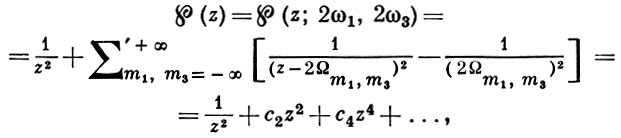
(1)
где 2Ωm1,m3 = 2m1ω1 + 2m3ω3 и целые числа m1, m3 пробегают все значения, кроме пары m1 - m3 = 0. Функция ℘(z) есть четная эллиптич. функция порядка 2, имеющая в каждом параллелограмме периодов единственный полюс 2-го порядка с нулевым вычетом. Ее производная ℘'(z) есть нечетная эллиптич. функция порядка 3 с теми же примитивными периодами; ℘'(z) имеет простые нули в точках, конгруэнтных 2ω1, 2ω2 = 2ω1 + 2ω3, 2ω3. Наиболее важное свойство функции ℘(z) состоит в том, что любая эллиптич. функция с данными примитивными периодами 2ω1, 2ω3 может быть представлена в виде рациональной функции от ℘(z) и ℘'(z), т. е. ℘(z) и ℘'(z) являются образующими алгебраич. поля эллиптич. функций с данными периодами. Среди однопериодических тригонометрич. функций аналогом функции ℘(z) служит 1/sin2z.
Функция ℘(z) удовлетворяет дифференциальному уравнению
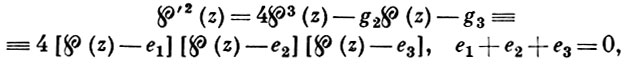
(2)
в к-ром модулярные формы
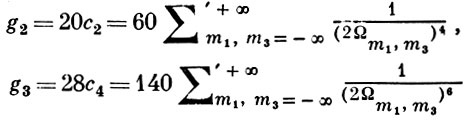
наз. относительными инвариантами, а величины е1 = ℘(2ω1), е2 = ℘(2ω2), е3 = ℘(2ω3) -иррациональными инвариантами функции ℘(z). Абсолютным инвариантом функции ℘(z) наз. всякая рациональная функция от j = g32/g23 или от J = g32/Δ, где Δ = g32 - 27g23 есть дискриминант. Имеется в виду инвариантность относительно модулярных преобразований (см. Модулярная функция). В приложениях обычно g2 и g3 - действительные; если при этом Δ > 0, то е1, е2, е3 - также все действительные. Уравнение (2) показывает, что ℘(z) может быть определена как обращение эллиптического интеграла I рода в нормальной форме Вейерштрасса:
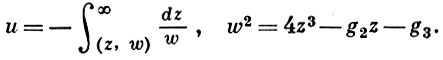
Функция ℘(z) отображает взаимно однозначно и конформно параллелограмм периодов на канонически разрезанную двулистную компактную риманову поверхность F с точками ветвления е1, е2, е3, ∞ рода 1; поверхность F иногда наз. эллиптическим образом. На главной накрывающей поверхности F указанный интеграл I рода однозначен и является униформизирующей переменной для F.
Эллиптич. интеграл II рода поля эллиптич. функций с данными периодами 2ω1, 2ω3 при этой униформизации переходит в дзета-функцию (ζ-функцию) Вейерштрасса ζ(z), определяемую рядом
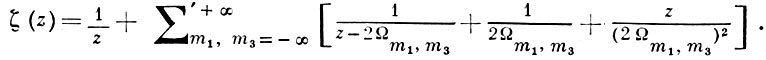
(3)
Функция ζ(z) - нечетная мероморфная функция, связанная с ℘(z) соотношением ζ'(z) = -℘(z); она не является периодической и при добавлении периодов преобразуется по закону ζ(z ± 2ωi) = ζ(z) ± 2ηi, где ηi = ζ(ωi). При этом между ω1, ω3, η1, η3 имеет место соотношение Лежандра
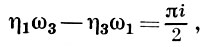
равносильное соотношению между полными эллиптич. интегралами:
EK' + Е'K - KK' = π/2.
Произвольная эллиптич. функция f(z) с данными периодами 2ω1, 2ω3 выражается через ζ(z) по формуле Эрмита:
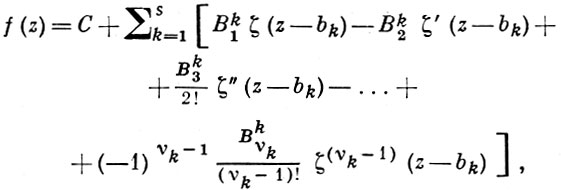
(4)
где С - постоянная, b1, b2, ..., bs - полная система полюсов функции f(z), числа Bk1, Вk2, ..., Bkνk - коэффициенты главной части разложения Лорана функции f(z) в окрестности полюса bk. Разложение (4) есть аналог разложения произвольной рациональной функции на простейшие дроби. Среди тригонометрич. функций аналогом функции ζ(z) является ctg z.
Сигма-функция (σ-функция) Вейерштрасса σ(z) определяется как бесконечное произведение
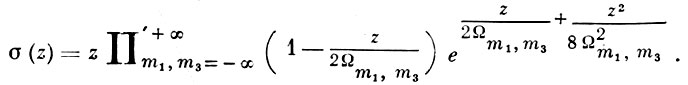
Функция σ(z) есть нечетная целая функция с нулями 2Ωm1, m3, связанная с функциями ℘(z) и ζ(z) соотношениями:
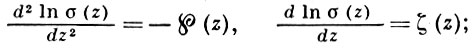
она не является двоякопериодической; имеют место тождества:
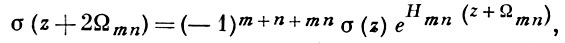
где
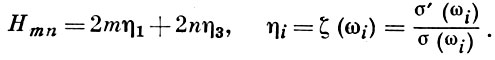
Произвольная эллиптич. функция f(z) с периодами 2ω1; 2ω3 выражается через σ(z) в виде:
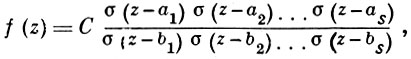
где С - постоянная; а1, а2, ..., аs, b1, b2, ..., bs - нулевая полная система нулей и полюсов функции f(z). Среди тригонометрич. функций аналогом функции σ(z) является sin z.
В теории Вейерштрасса имеют также значение сигма-функции с индексами:
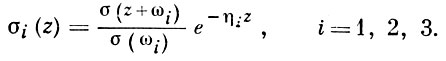
Функции σ(z), σ1(z), σ2(z), σ3(z) выражаются через тета-функции 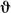 0(v),
0(v), 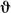 1(v),
1(v), 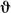 2(v),
2(v),  3(v) (см. Якоби эллиптические функции), а функция ℘(z) просто выражается через σ(z), σ1(z), σ2(z), σ3(z), что составляет вычислительный базис функций Вейерштрасса. Можно получить и непосредственное выражение В. э. ф. через эллиптич. функции Якоби, напр. в виде:
3(v) (см. Якоби эллиптические функции), а функция ℘(z) просто выражается через σ(z), σ1(z), σ2(z), σ3(z), что составляет вычислительный базис функций Вейерштрасса. Можно получить и непосредственное выражение В. э. ф. через эллиптич. функции Якоби, напр. в виде:
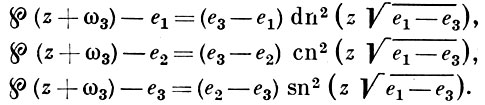
В прикладных вопросах обычно заданы относительные инварианты g2, g3. При этом для вычисления примитивных периодов 2ω1, 2ω3 используется абсолютный инвариант J = g32/Δ, к-рый является модулярной функцией от отношения периодов τ = ω3/ω1 (см. также Модулярная функция).
Лит.: [1] Wеiеrstrаss К., Mathematische Werke. Bd 1-2, В., 1894-95; [2] Schwarz Н. A., Formeln und Lehrsatze zum Gebrauche der elliptischen Funktionen, 2 Aufl., В., 1893; [3] Гурвиц А., Курант P., Теория функций, M., 1968, ч. 2: [4] Уиттекер Э. Т., Ватсон Дж. Н., Курс современного анализа, пер. с англ., 2 изд., ч. 2, М., 1963, гл. 20; [5] Ахиезер Н. И., Элементы теории эллиптических функций, 2 изд., М., 1970.
Е. Д. Соломенцев.
Источники:
- Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'