ВЕЙЕРШТРАССА ТЕОРЕМА

ВЕЙЕРШТРАССА ТЕОРЕМА - 1) В. т. о бесконечном произведении [1]: для любой наперед заданной последовательности точек плоскости ℂ комплексного переменного z

0, ..., 0, α₁, α₂, ..., 0 < |α_k| ≤ |α_k+1|, k = 1, 2, ...; lim_k→∞ |α_k| = ∞, (1)

существует целая функция, имеющая нулями точки α_k этой последовательности и только их. Эта функция может быть построена в виде канонического произведения

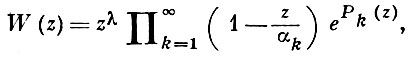
(2)

где λ - кратность нуля в последовательности (1), а

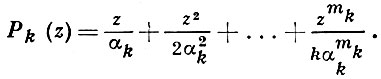
Множители

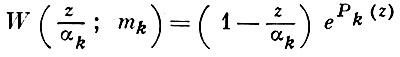
наз. первичными, или примарными, множителями Вейерштрасса. Показатели m_k в них выбираются так, чтобы обеспечить сходимость произведения (2), напр., выбор m_k = k обеспечивает сходимость (2) для любой последовательности вида (1).

Из этой теоремы вытекает также, что любая целая функция f(z) с нулями (1) имеет вид

f(z) = e^g(z)W(z),

где W(z) - канонич. произведение (2), a g(z) - нек-рая целая функция (см. также Адамара теорема о целых функциях).

В. т. о бесконечном произведении обобщается на случай произвольной области D⊂ℂ: какова бы ни была последовательность точек {α_k} ⊂ D, не имеющая предельных точек в D, существует голоморфная в D функция f, имеющая нули в точках и только в них.

Утверждение теоремы в части, касающейся существования целой функции с произвольно заданными нулями, обобщается следующим образом на функции многих комплексных переменных: пусть каждой точке а комплексного пространства ℂⁿ, n ≥ 1, поставлена в соответствие нек-рая ее окрестность U_α и голоморфная в U_α функция f_α. При этом, если пересечение U_α ∩ U_β окрестностей точек α, β ∈ ℂⁿ не пусто, то отношение f_αf_β ≠ 0 в U_α ∩ U_β есть голоморфная функция. При этих условиях существует целая функция f в ℂⁿ такая, что отношение f/f_α есть голоморфная функция в любой точке α ∈ ℂⁿ. Это утверждение известно как вторая теорема Кузена (см. также Кузена проблемы).

Лит.: [1] Weierstrass К., Math. Werke, Bd 2, В., 1895; [2] Маркушевич А. И., Теория аналитических функций, т. 2, 2 изд., М., 1968; [3] Шабат Б. В., Введение в комплексный анализ, ч. 1-2, 2 изд., М., 1976.

Е. Д. Соломенцев.

2) В. т. о приближении функций: для любой действительной непрерывной на отрезке [а, b] функции f(x) существует последовательность алгебраич. многочленов Р₀(х), Р₁(х), ..., Р_n(х), равномерно сходящаяся на [а, b] к функции f(х); установлена К. Вейерштрассом [1].

Аналогичные результаты имеют место во всех пространствах L_p[a, b]. Усилением этой В. т. является Джексона теорема.

Эта теорема справедлива также для действительных непрерывных 2π-периодич. функций и тригонометрич. полиномов или, напр., для действительных функций, непрерывных на ограниченной замкнутой области m-мерного пространства, и многочленов от m переменных. Об обобщениях см. Вейерштрасса-Стоуна теорема. О приближении функций комплексного переменного многочленами см. [3].

Лит.: [1] Weierstrass К., «Sitzungsber. Acad. Веrlin», 1885, S. 633-9, 789-805; [2] Ахиезер Н. И., Лекции по теории аппроксимации, 2 изд., М., 1965; [3] Шабат Б. В., Введение в комплексный анализ, ч. 1-2, 2 изд., М., 1976.

Ю. Н. Субботин.

3) В. т. о равномерно сходящихся рядах аналитических функций [1]: если члены ряда

(*)

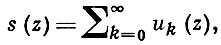
равномерно сходящегося внутри области D комплексной плоскости ℂ, являются аналитич. функциями в D, то его сумма s(z) также является аналитич. функцией в D. Кроме того, ряды

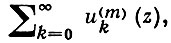
полученные m-кратным почленным дифференцированием ряда (*) при любом m, также равномерно сходятся внутри D к производным s^m(z) от суммы ряда (*). Эта теорема обобщается на ряды аналитич. функций многих комплексных переменных, равномерно сходящиеся внутри области D комплексного пространства ℂⁿ, n ≥ 1, причем ряды, составленные из частных производных любого порядка от членов ряда (*), сходятся равномерно к соответствующим частным производным от суммы ряда:

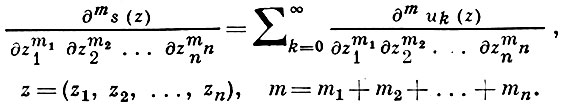
E. Д. Соломенцев.

4) В. т. о равномерной сходимости на границе области [1]: если члены ряда

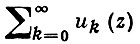
непрерывны в замкнутой ограниченной области D̄ комплексной плоскости ℂ и аналитичны в D, то из равномерной сходимости этого ряда на границе области D вытекает его равномерная сходимость в замкнутой области D̄.

Это свойство рядов, составленных из аналитич. функций, остается справедливым и для аналитич. или гармонич. функций, заданных соответственно в областях комплексного пространства ℂⁿ, n ≥ 1, или евклидова пространства Еⁿ, n ≥ 2. Вообще, оно остается справедливым в любой ситуации, где применим максимума модуля принцип.

Лит.: [1] Weierstrass К., Abhandlungen aus der Funktionenlehre, В., 1860; Math. Werke, Bd 2, В., 1895; [2] Уиттекер Э. Т., Ватсон Дж. Н., Курс современного анализа, 2 изд., пер. с англ., ч. 1, М., 1963, гл. 3; [3] Маркушевич А. И., Теория аналитических функций, 2 изд., т. 1, М., 1967, гл. 3, т. 2, М., 1968, гл. 7.

Е. Д. Соломенцев.

5) В. т. подготовительная - теорема, полученная К. Вейерштрассом [1] и сформулированная им первоначально в 1860 как подготовительная лемма при доказательстве существования и аналитичности неявной функции комплексного переменного, определяемой уравнением f(z, w)=0, левая часть к-рого есть голоморфная функция двух комплексных переменных. Эта теорема обобщает на функции многих комплексных переменных следующее важное свойство голоморфных функций одного комплексного переменного: если f(z) -голоморфная функция от z в окрестности начала координат и f(0) = 0, f(z) ≣ 0, то она представима в виде f(z) = z^s g(z), где s - кратность нуля f(z) в начале координат, s ≥ 1, а голоморфная функция g(z) отлична от нуля в нек-рой окрестности начала.

Формулировка подготовительной теоремы Вейерштрасса для функций n комплексных переменных, n ≥ 1. Пусть

f(z) = f(z₁, ..., z_n)

- голоморфная функция от z = (z₁, ..., z_n) в поликруге

U = {z; |z_i| < a_i, i = 1, 2, ..., n},

причем

f(0) = 0, f(0, 0, ..., 0, z_n) ≣ 0.

Тогда в некотором поликруге

V = {z; |z_i| < b_i ≤ a_i, i = 1, 2, ..., n}

функция f(z) представима в виде

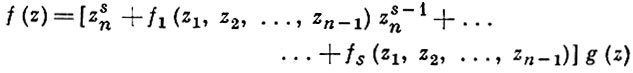
где s - кратность нуля функции

f(z_n) = f(0, 0, ..., 0, z_n)

в начале координат, s ≥ l; функции f_j(z₁, z₂, ..., z_n-1) голоморфны в поликруге

V = {(z₁, z₂, ..., z_n-1); |z_i| < b_i, i = 1, 2, ..., n-1}, f_j(0, 0, ..., 0) = 0, j = 1, 2, .., s;

функция g(z) голоморфна и не обращается в нуль в поликруге V. Функции f_j(z₁, z₂, ..., z_n-1), j = 1, 2, ..., s, и g(z) определяются условиями теоремы однозначно.

Вместо начала координат можно принять, изменив соответственно формулировку, любую точку а = (a₁, a₂, ..., a_n) комплексного пространства ℂⁿ. Из подготовительной В. т. вытекает, что при n > 1, в отличие от случая одного комплексного переменного, во всякой окрестности любого нуля голоморфной функции находится бесконечное множество других ее нулей.

Подготовительная В. т. имеет чисто алгебраич. природу и может быть сформулирована для формальных степенных рядов. Пусть ℂ[[z₁, z₂, ..., z_n]] - кольцо формальных степенных рядов от переменных z₁, z₂, ..., z_n с коэффициентами из поля комплексных чисел ℂ; f - такой ряд из этого кольца, члены к-рого имеют низшую степень s ≥ 1, причем существует член вида cz^sn, с ≠ 0. Тогда f можно представить в виде

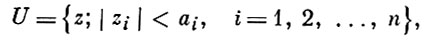
где f₁, f₂, ..., f_s - ряды из кольца C[[z₁, z₂, ..., z_n]], свободные члены к-рых равны нулю, a g - ряд из ℂ[[z₁, z₂, ..., z_n]] со свободным членом, отличным от нуля. Формальные степенные ряды f₁, f₂, ..., f_s и g определяются по f однозначно.

Иногда подготовительной В. т. наз. следующее утверждение о делении: пусть ряд

f ∈ ℂ[[z₁, z₂, ..., z_n]]

удовлетворяет только что указанным условиям, g -любой ряд из ℂ[[z₁, z₂, ..., z_n]]. Тогда существуют такой ряд

h ∈ ℂ[[z₁, z₂, ..., z_n]]

и такие ряды

a_j ∈ ℂ[[z₁, z₂, ..., z_n-1]], a_j(0, 0, ..., 0) = 0, j = 0, 1, 2, ..., s-1,

для к-рых выполняется равенство

g = hf + a₀ + a₁z_n + ... + a_s-1z_n^s-1

Подготовительная В. т. верна также для колец формальных ограниченных рядов. Она дает способ индуктивного перехода, напр., от ℂ[[z₁, z₂, ..., z_n-1]] к ℂ[[z₁, z₂, ..., z_n]]. Таким образом удается установить нек-рые свойства колец ℂ[z₁, z₂, ..., z_n] и ℂ[[z₁, z₂, ..., z_n]], напр., нётеровость и факториальность. Имеется обобщение этой теоремы для дифференцируемых функций (см. [6]).

Лит.: [1] Weierstrass К., Abhandlungen aus der Funktionenlehre, В., 1860; Math. Werke, Bd 2, В., 1895; [2] Шабат Б. В., Введение в комплексный анализ, ч. 1-2, 2 изд., М., 1976; [3] Бохнер С., Мартин У., Функции многих комплексных переменных, пер. с англ., М., 1951, гл. 9; [4] Ганнинг Р., Росси X., Аналитические функции многих комплексных переменных, пер. с англ., М., 1969, гл. 2; [5] Шафаревич И. Р., Основы алгебраической геометрии, М., 1972, гл. 2; [6] Мальгранж Б., Идеалы дифференцируемых функций, пер. с англ., М., 1968.

Е. Д. Соломенцев.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.