ВЕЙЕРШТРАССА ПРИЗНАК

ВЕЙЕРШТРАССА ПРИЗНАК равномерной сходимости - утверждение, дающее достаточные условия равномерной сходимости ряда или последовательности функций посредством сравнения их с соответствующими числовыми рядами и последовательностями; установлен К. Вейерштрассом [1]. Если для ряда

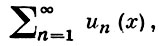
составленного из действительных или комплексных функций, определенных на нек-ром множестве Е, существует числовой сходящийся ряд

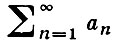
такой, что

|u_n(x)| ≤ a_n, n = 1, 2, ...,

то исходный ряд сходится равномерно и абсолютно на множестве Е. Напр., ряд

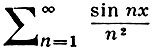
абсолютно сходится на всей действительной оси, поскольку

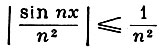
и ряд

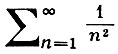
сходится.

Если для последовательности действительных или комплексных функций f_n(x), n = 1, 2, ..., сходящейся на множестве Е к функции f(x), существует бесконечно малая числовая последовательность α_n, такая, что |f(x) - f_n(x)| ≤ α_n, х ∈ Е, n = 1, 2, ..., то данная последовательность сходится на множестве Е равномерно. Напр., последовательность

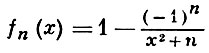
равномерно на всей действительной оси сходится к функции f(x) = 1, так как

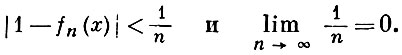
В. п. равномерной сходимости переносится на функции, значения к-рых лежат в нормированных линейных пространствах.

Лит.: [1] Weierstrass К., Abhandlungen aus der Funktionenlehre, В., 1886; Math. Werke, Bd 2, В., 1895.

Л. Д. Кудрявцев.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.