ВЕЙБУЛЛА РАСПРЕДЕЛЕНИЕ

ВЕЙБУЛЛА РАСПРЕДЕЛЕНИЕ - специальный вид распределения вероятностей случайных величин X_w; характеризуется функцией распределения

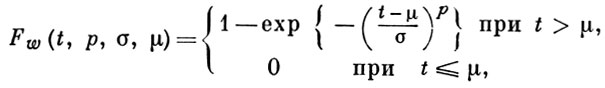
где р - параметр формы кривой распределения, σ -параметр масштаба, μ - параметр сдвига. Семейство распределений (*) названо по имени В. Вейбулла [1], впервые использовавшего его для аппроксимации экспериментальных данных о прочности стали на разрыв при усталостных испытаниях и предложившего методы оценки параметров распределения (*). В. р. принадлежит к асимптотич. распределению третьего типа крайних членов вариационного ряда. Оно широко используется для описания закономерностей отказов шарикоподшипников, вакуумных приборов, элементов электроники. Частными случаями В. р. являются экспоненциальное (р = 1) и рэлеевское (р = 2) распределения. Кривые функции распределения (*) не принадлежат семейству распределений Пирсона. Имеются вспомогательные таблицы для вычислений функции распределения Вейбулла (см. [2]). При р = 0 квантиль уровня q равна σ[-ln (1 - q)]^1/p,

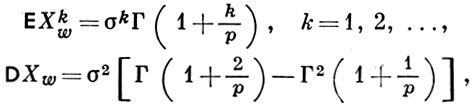
где Г(х) - гамма-функция; коэффициент вариации, асимметрия и эксцесс не зависят от σ, что облегчает их табулирование и создание вспомогательных таблиц для получения оценок параметров. При р ≥ 1 В. р. унимодально, мода равна σ(р - 1)^1/p функция опасности отказов λ(t) = pt^p-1/σ^p не убывает. При р < 1 функция λ(t) монотонно убывает. Можно построить так. наз. вероятностную бумагу Вейбулла (см. [3]). На ней F_w(t, р, σ, 0) трансформ» руется в прямую, при μ > 0 образ F_w(t, р, σ, μ) имеет вогнутость, а при μ < 0 - выпуклость. Оценки параметров В. р. по методу квантилей приводят к уравнениям существенно более простым, чем по методу максимального правдоподобия. Совместная асимптотич. эффективность оценок параметров р и σ (при μ = 0) по методу квантилей максимальна (и равна 0,64) при использовании квантилей уровня 0,24 и 0,93. Функция распределения (*) хорошо аппроксимируется функцией распределения логнормального распределения

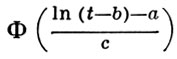
(Ф (х) - функция распределения нормированного нормального распределения, -∞ < b < ∞, -∞ < а < ∞, с > 0):

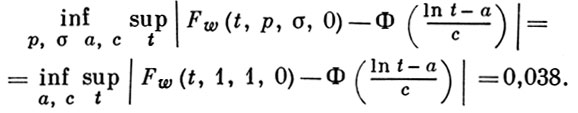
Лит.: [1] Weibull W., A statistical theory of the strength of materials, Stockh., 1939; [2] Гнеденко Б. В., Беляев Ю. К., Соловьев А. Д., Математические методы в теории надежности, М., 1965; [3] Jоhnson L., The statistical treatment of fatigue experiments, Amst., 1964; [4] Крамер Г., Математические методы статистики, пер. с англ., 2 изд., М., 1975.

Ю. К. Беляев, Е. В. Чепурин.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.