ВЕБЕРА ФУНКЦИЯ

ВЕБЕРА ФУНКЦИЯ - функция

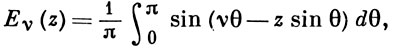
где z - комплексное, ν - действительное, удовлетворяющая неоднородному Бесселя уравнению:

z²y'' + zy' + (z² - ν²) у = -π^-1[(z + ν) + (z - ν)cos νπ].

Для нецелых ν справедливо разложение

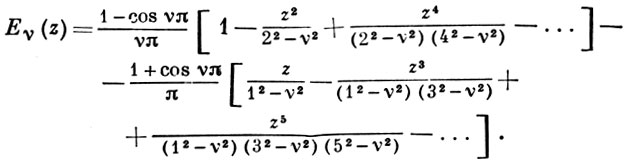
При |z| → ∞ и |arg z| < π/2 имеет место асимптотич. разложение

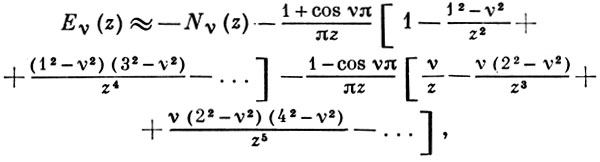
где N_ν - Неймана функция. Если ν не целое, то В. ф. связана с Ангера функцией J_ν(z) следующими соотношениями:

sin νπ ⋅ J_ν(z) = cos νπ E_ν(z) - E_-ν(z), sin νπ ⋅ E_ν(z) = J_-ν(z) - cos νπ ⋅ J_ν(z).

В. ф. впервые изучалась Г. Вебером [1].

Лит.: [1] Weber Н. F., «Zürich Vierteljahresschrift», 1879, Bd 24, S. 33-76; [2] Ватсон Г. Н., Теория бесселевых функций, пер. с англ., ч. 1, М., 1949.

А. П. Прудников.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.