ВВЕДЕНИЯ ПАРАМЕТРА МЕТОД

ВВЕДЕНИЯ ПАРАМЕТРА МЕТОД - метод представления правой части системы дифференциальных уравнений

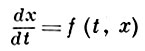
(1)

в виде

f(t, x) = f₀(t, x) + εg(t, х), ε = 1, g = f - f₀,

где f₀ означает главную (в том или ином смысле) часть вектор-функции f, a g - совокупность членов второстепенного значения. Разбиение f на f₀ и g обычно диктуется физич. или аналитич. смыслом задачи, описываемой системой (1). Наряду с (1) рассматривают систему с параметром

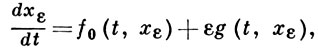
(2)

к-рая при ε = 0 обращается в вырожденную систему

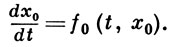
(3)

Если f(t, х) и g(t, х) голоморфны в окрестности точки (τ, ξ), то система (2) при достаточно малых по модулю значениях ε имеет решение x_ε(t; τ, ξ), х_ε(τ; τ, ξ) = ξ, к-рое в окрестности начальных значений (τ, ξ) представимо в виде ряда по степеням ε:

x_ε(t; τ, ξ) = x₀(t; τ, ξ) + εφ₁(t; τ, ξ) + ... + εⁿφ_n(t; τ, ξ) + ..., φ_k(τ; τ, ξ) = 0 (4)

(в нек-рых случаях для φ_k задают и ненулевые начальные значения). Если ряд (4) сходится при ε = 1, то он доставляет решение системы (1) с начальными значениями (τ, ξ). Для фактического построения коэффициентов φ_n достаточно располагать общим решением системы (3) и частным решением z(t; τ, 0) любой системы

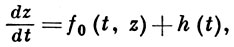
где h(t) голоморфна в окрестности t = τ.

В частности, все φ_n последовательно определяются с помощью квадратур, если f₀(f, х) = Ах, где А - постоянная матрица.

Особенно широко В. п. м. используется в теории нелинейных колебаний [3] при построении периодич. решений системы (1). См. также Малого параметра метод. В. п. м. был использован П. Пенлеве (P. Painlevé) для выделения дифференциальных уравнений 2-го порядка, решения к-рых не имеют подвижных критических особых точек (см. Пенлеве уравнение). Справедливо утверждение: системами с неподвижными критич. точками могут быть лишь такие системы (1), к-рые после введения подходящего параметра е имеют в качестве вырожденных систем (3) системы без подвижных критич. особенностей. В. п. м. широко применяется для построения новых классов существенно нелинейных дифференциальных систем (1) без подвижных критических особых точек и для исследования систем указанных классов (см. Особая точка дифференциального уравнения).

Лит.: [1] Пуанкаре А., Избр. труды, пер. с франц., М., 1971, т. 1, с. 9-456; [2] Ляпунов А. М., Собр. соч., М.-Л., 1956, т. II, с. 7-263; [3] Боголюбов Н. Н., Митропольский Ю. А., Асимптотические методы в теории нелинейных колебаний, 4 изд., М., 1974; [4] Голубев В. В., Лекции по аналитической теории дифференциальных уравнений, 2 изд., М.-Л., 1950; [5] Еругин Н. П., «Дифференц. уравнения», 1967, т. 3, № 11, с. 1821-63.

Ю. С. Богданов.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.