ВАРИНГА ПРОБЛЕМА

ВАРИНГА ПРОБЛЕМА - проблема теории чисел, сформулированная Э. Варингом (Е. Waring) в 1770 в следующем виде: всякое натуральное число есть сумма четырех квадратов, девяти кубов, девятнадцати четвертых степеней. Другими словами: для любого n ≥ 2 существует такое k = k(n), зависящее только от n, что любое натуральное число есть сумма k n-х степеней неотрицательных целых чисел. Первое общее решение В. п. с очень грубой оценкой величины k в зависимости от n дано в 1909 Д. Гильбертом (D. Hilbert), в связи с чем В. п. иногда наз. проблемой Гильберта-Варинга. Если через J_k,n(N) обозначить число решений в целых неотрицательных числах уравнения

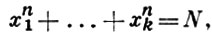
(1)

то теорема Гильберта утверждает, что существует K = k(n), для к-рого J_k,n(N) ≥ 1 при любом N ≥ 1. В 1928 Г. X. Харди и Дж. И. Литлвуд (G. Н. Hardy, J. Е. Littlewood), применив к В. п. круговой метод, доказали, что при k ≥ (n - 2) 2^n-1 + 5 для J_k,n(N) имеет место асимптотич. формула вида

J_k,n(N) = AN^k/n-1 + O(N^k/n-1-γ), (2)

где А = А(N) ≥ с₀ > 0, а с₀ и γ > 0 некоторые постоянные. Следовательно, при N ≥ N₀(n) уравнение (1) имеет решение. В связи с этим результатом возникли три проблемы: установить порядок трех величин G(n), g(n), k₀(n) - наименьших целых чисел, для к-рых: а) уравнение (1) разрешимо при k ≥ G(n) и N ≥ N₀(n); б) уравнение (1) разрешимо при k ≥ g(n) и N ≥ 1; в) для величины J_k,n(N) ПРИ k ≥ k₀(n) имеет место асимптотич. формула (2).

а) Известно, что G(n) ≥ n+1. В 1934 И. М. Виноградов при помощи созданного им метода доказал, что

G(n) ≤ 3n(ln n + 9).

Кроме того, имеется много результатов относительно G(n) для небольших значений n: G(4) = 16 (X. Давенпорт, Н. Davenport, 1939), G(3) = 7 (Ю. В. Линннк, 1942).

б) В 1936 Л. Диксон и С. Пиллаи (L. Dickson, S. Pillai), применив Виноградова метод, доказали, что

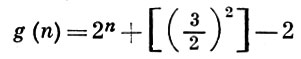
для всех n > 6, для к-рых

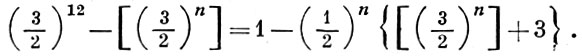
Последнее же условие доказано К. Малером (К. Mahler) в 1957 для всех достаточно больших n.

в) Наилучший результат принадлежит И. М. Виноградову, к-рый доказал, что

k₀(n) ≤ 4n² ln n.

Элементарное доказательство В. п. дано Ю. В. Линником в 1942. Существует много различных обобщений В. п. (переменные пробегают нек-рое подмножество множества натуральных чисел; вместо одночленов xⁿ₁, ..., xⁿ_n в представлении числа N рассматриваются многочлены f₁(x₁), f₂(x₂), ..., f_k(x_k); вместо уравнения (1) рассматривается сравнение и т. д.).

Особое значение В. п. состоит в том, что при ее решении созданы мощные методы аналитической теории чисел.

Лит.: [1] Виноградов И. М., Избранные труды, М., 1952; [2] его же, Метод тригонометрических сумм в теории чисел, М., 1971; [3] Xуа Ло-ген, Метод тригонометрических сумм и его применение в теории чисел, пер. с нем., М., 1964; [4] Делоне Б. Н., Петербургская школа теории чисел, М.-Л., 1947; [5] Xинчин А. Я., Три жемчужины теории чисел, 2 изд., М.- Л., 1948.

А. А. Карацуба.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.