ВАРИАЦИЯ ФУНКЦИИ

ВАРИАЦИЯ ФУНКЦИИ - числовая характеристика функции одного действительного переменного, связанная с ее дифференциальными свойствами.

1) Пусть f(x) - функция действительного переменного х, заданная на отрезке [а, b]; ее вариация V^b_a(f) есть тонная верхняя грань сумм вида

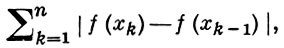
где а = х₀ < х₁ < ... < x_n = b - произвольная система точек из [а, b]. Это определение предложено К. Жорданом [1]. Если V^b_a(f) < ∞, то говорят, что функция f(x) имеет ограниченную (конечную) вариацию на отрезке [а, b], а класс всех таких функций обозначают через V[а, b] или просто через V. Функция f(x) принадлежит классу V[а, b] тогда и только тогда, когда она может быть представлена в виде f(х) = f₁(x) - f₂(x), где f₁ и f₂ - возрастающие (убывающие) на [а, b] функции (Жордана разложение функции ограниченной вариации). Сумма, разность и произведение двух функций класса V[а, b] также есть функция класса V [а, b]. Это справедливо и для частного двух функций класса V[а, b], если модуль знаменателя превосходит положительную постоянную на отрезке [а, b]. Каждая функция класса V[а, b] ограничена и может иметь не более чем счетное множество точек разрыва, причем все они 1-го рода. Все эти свойства функций класса V [a, b] установлены К. Жорданом [1] (см. также [2], с. 234-38).

Функции f(x) класса V [а, b] почти всюду дифференцируемы на [а, b] и для них имеет место разложение

f(x) = A(x) + S(x) + D(x),

где А(х) - абсолютно непрерывная, S(х) - сингулярная функция, a D(х) - функция скачков (Лебега разложение функции ограниченной вариации). Это разложение единственно, если f(a) = A(а) (см. [3] и [2], с. 290).

Первоначально класс V [а, b] был введен К. Жорданом в связи с обобщением Дирихле признака сходимости рядов Фурье кусочно монотонных функций. К. Жор-дан доказал, что ряды Фурье 2π-периодич. функций класса У [0, 2π] сходятся в каждой точке действительной оси. Однако в дальнейшем функции ограниченной вариации нашли широкое применение в различных областях математики, особенно в теории интеграла Стилтьеса.

Иногда рассматриваются классы V_Ф[а, b], к-рые определяются следующим образом. Пусть Ф(u) (u ≥ 0, Ф(0) = 0) положительная при u > 0 монотонно возрастающая непрерывная функция. Обозначим через V^b_Фa(f) точную верхнюю грань сумм вида

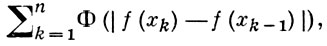
где а = x₀ < x₁ < ... < x_n = b - произвольное разбиение отрезка [а, b]. Величина V^b_Фa(f) наз. Ф-вариацией функции f(x) на отрезке [а, b]. Если V^b_Фa(f) < ∞, то говорят, что функция f(x) имеет ограниченную Ф-вариацию на отрезке [a, b], а класс всех таких функций обозначается через V_Ф[a, b] или просто через V_Ф (см. [4], с. 287). При Ф(u) = u получается класс V[a, b] К. Жордана, а при Ф(u) = u^p(1 < р < ∞) - классы V_p Н. Винера [5]. Определение класса V_Ф[а, b] предложено Л. Юнг [6].

Если

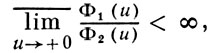
тo

V_Ф2[а, b] ⊂ V_Ф1[а, b].

В частности,

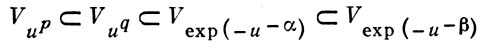
при 1 ≤ р < q < ∞, 0 < α < β < ∞, причем эти вложения строгие.

Лит.: [1] Jordan С. «С. r. Acad. sci.», 1881, t. 92, № 5, p. 228-30; [2] Haтaнсон И. П., Теория функций вещественной переменной, 2 изд., М., 1957; [3] Лебег А., Интегрирование и отыскание примитивных функций, (пер. с франц.), М.-Л., 1934; [4] Бари Н. К., Тригонометрические ряды, М., 1961; [5] Wiener N., «Massachusetts J. Math, and Phys.», 1924, v. 3, p. 72-94; [6] Yоung L. С., «C. r. Acad. sci.», 1937, t. 204, № 7, p. 470-72.

Б. И. Голубов.

2) Для функции нескольких переменных имеются различные определения вариаций (Арцела вариация, Витали вариация, Пьерпонта вариация, Тонелли плоская вариация, Фреше вариация, Харди вариация). Очень плодотворным оказалось также следующее определение (см. [1]), основанное на использовании Банаха индикатрисы. Пусть действительнозначная функция f(x) = f(x₁, ..., x_n) задана и измерима по Лебегу на n-мерном кубе Q_n. Вариацией V_k(f) порядка k (k = 1, 2, ..., n) функции f(x) на кубе Q_n наз. число

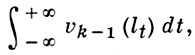
где v_k-1(l_t) обозначает (k-1)-ю вариацию множества l_t = {х : x ∈ Q_n, f(x) = t), а интеграл понимается в смысле Лебега. Это определение позволяет перенести на функции нескольких переменных многие свойства функций ограниченной вариации одного переменного. Напр.:

а) V_n(f+g) ≤ V_n(f) + V_n(g); V_k(cf) = |c|V_k(f), k = 1, 2, ..., n.

б) Если последовательность функций f_s(x) (s = 1, 2, ...) сходится к f(x) равномерно на Q_n, то

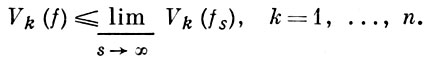
в) Если функция f(x) непрерывна на Q_n и все ее вариации конечны, то f(x) почти всюду имеет полный дифференциал.

г) Если функция f(x) абсолютно непрерывна на Q_n, то

V_n(f) = ∫_Qn |grad f| dx.

д) Если функция f(x) непрерывна на кубе Q_n со стороной 2π, имеет конечные вариации всех порядков на кубе Q_n и может быть периодически продолжена с периодом 2π по каждому аргументу х_k, k = 1, ..., n на все n-мерное пространство, то ее ряд Фурье равномерно сходится к ней на Q_n по Прингсхейму.

Достаточные условия конечности вариаций: если функция f(x) имеет на кубе Q_n непрерывные производные всех порядков до (n-k+1)-го включительно, то ее вариация порядка k конечна. Эта теорема является окончательной в том смысле, что условия на гладкость не улучшаемы ни при одном k.

Лит.: [1] Витушкин А. Г., О многомерных вариациях, М., 1955.

А. Г. Витушкин.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.