ВАРИАЦИЯ ОТОБРАЖЕНИЯ

ВАРИАЦИЯ ОТОБРАЖЕНИЯ - числовая характеристика отображения, связанная с его дифференциальными свойствами. Определена С. Банахом [1]. Ниже дается определение лишь для двумерного случая. Рассмотрим отображение

α : x = f (u, v), u = φ (u, v),

где f (u,v) и φ (u, v) - непрерывные на квадрате D₀ = [0,1] × [0,1] функции. Говорят, что отображение α имеет ограниченную вариацию, если существует число М > 0 такое, что для любой последовательности неперекрывающихся квадратов Dⁱ ⊂ D_o(i = 1, 2, ...) со сторонами, параллельными осям координат u, v, справедливо неравенство

∑_i mes Dⁱ_xy ≤ M,

где Е_xy обозначает образ множества E ⊂ D₀ при отображении α, a mes Е - плоскую меру Лебега множества Е. При этом численное значение V(α) В. о. а может быть определено различными способами. Напр., пусть отображение а имеет ограниченную вариацию. Тогда вариация V(α) может быть определена по формуле

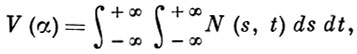
где N(s, t) - число решений системы f(u, v) = s, φ(u, v) = t (индикатриса Банаха отображения α).

Если отображение α имеет ограниченную вариацию, то почти всюду на D₀ существует обобщенный якобиан J(Р) (P⊂D₀), к-рый интегрируем на D₀. При этом

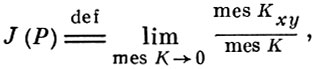
где K ⊂ D₀ - квадрат, содержащий точку P ⊂ D₀, стороны к-рого параллельны осям u, v (см. [2]).

Лит.: [1] Ваnасh S., «Fundam. math.», 1925, t. 7, p. 225-36; [2] Кудрявцев Л. Д., в сб.: Метрические вопросы теории функций и отображений, в. 1, К., 1969, с. 34-108.

Б. И. Голубов.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.