ВАРИАЦИЯ МНОЖЕСТВА

ВАРИАЦИЯ МНОЖЕСТВА - число, характеризующее k-мерную протяженность множества в n-мерном евклидовом пространстве. Нулевая вариация V₀(E) замкнутого ограниченного множества Е есть число компонент этого множества.

Для простейшего случая плоскости линейная вариация множества (то есть В. м. порядка 1) V₁(Е) есть интеграл

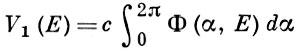
от функции

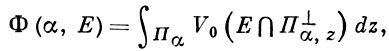
где интегрирование ведется по прямой П_α, проходящей через начало координат, α - угол наклона П_α к фиксированной оси и П^⊥_α,z - прямая, перпендикулярная к П_α и пересекающая ее в точке z. Нормирующая константа с выбирается так, чтобы вариация V₁(Е) отрезка Е совпадала с его длиной. Для достаточно простых множеств, напр. спрямляемых кривых, В. м. равна длине кривой. Для замкнутой области Е со спрямляемой границей Г линейная В. м. V₁(E) равна половине длины Г. Вторая В. м. (то есть В. м. порядка 2) есть двумерная мера множества Е и V_k(E) = 0 при k > 2.

Для n-мерного евклидова пространства вариацией V_i(E) порядка i = 0, 1, ..., n ограниченного замкнутого множества Е наз. интеграл

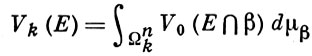
от нулевой вариации пересечения Е с (n-k)-мерной плоскостью β по пространству Ωⁿ_k всех (n-k)-мерных плоскостей из R_n, с Хаара мерой dμ_β, нормированной так, чтобы единичный k-мерный куб J_k имел В. м. V_k(J_k) = 1

В. м. V_n(E) совпадает с n-мерной мерой Лебега множества Е. Для выпуклых тел В. м. при надлежащей нормировке совпадает со смешанными объемами Минковского (см. [4]).

Свойства В. м. 1) Для E⊂R_n⊂R_n' В. м. V_k(Е) не зависит от того, вычисляется она для E⊂R_n или для E⊂R_n'.

2) В. м. выражаются индуктивно по формуле

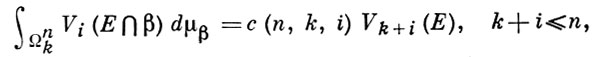
где с (n, k, i) - нормирующая константа.

3) Условие V_i(E) = 0 влечет V_i+1(E)=0.

4) В. м. (в известном смысле) не зависят друг от друга, т. е. для любой последовательности чисел a₀, ..., a_n, где а₀ > 0 - целое, 0 < а_i ≤ ∞, i = 1, ..., n-1; а_n = 0, можно построить множество E⊂R_n, для к-рого V_i(E) = a_i, i = 0, 1, ..., n.

5) V_i(E₁∪E₂) = V_i(E₁) + V_i(E₂), если Е₁ и Е₂ не пересекаются. В общем случае

V_i(E₁∪E₂) ≤ V_i(E₁) + V_i(E₂).

Для i = 0, 1, ..., n-1 В. м. V_i не монотонны, т. е. может оказаться, что V_i(E₁) < V_i(Е₂) для E₁ ⊃ E₂.

6) В. м. полунепрерывны, т. е. если последовательность замкнутых ограниченных множеств Е_k сходится (в смысле метрики уклонений) к множеству Е, то

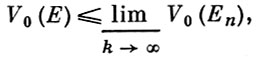
а если, к тому же, равномерно ограничены суммы V₀(E_k) + ... + V_i-1(E_k), то

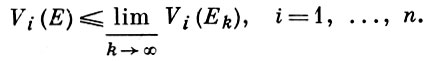
7) В. м. V_k(E) совпадаете k-мерной Хаусдорфа мерой множества Е, если V_k+1(Е) = 0, а

V₀(E) + ... + V_k(E) < ∞.

Эти условия выполняются, напр., для дважды гладких многообразий.

Понятие В. м. возникло в связи с исследованием решений системы Коши-Римана и в окончательной формулировке принадлежит А. Г. Витушкину. В. м. оказалась полезным аппаратом при решении нек-рых задач анализа, в частности при изучении суперпозиций функций многих переменных (см. [1]), а также в вопросах аппроксимации (см. [2]).

Лит.: [1] Витушкин А. Г., О многомерных вариациях, М., 1955; [2] его же, Оценка сложности задачи табулирования, М., 1959; [3] его же, «Докл. АН СССР», 1966, т. 166, № 5, с. 1022-25; [4] Леонтович А. М., Мельников М. С. «Тр. Моск. матем. об-ва», 1965, т. 14, с. 306-37; [5] Иванов Л. Д., «Матем. сб.», 1967, т. 72(114), № 3, с. 445-70; [6] его же, там же, 1969, т. 78(120), № 1, с. 85-100.

А. Г. Витушкин, Л. Д. Иванов.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.