ВАРИАЦИОННЫЕ ПРИНЦИПЫ

ВАРИАЦИОННЫЕ ПРИНЦИПЫ в теории функций комплексного переменного - положения, выявляющие закономерности изменения отображающих функций при определенных деформациях плоских областей.

Основным качественным В. п. является Линделёфа принцип, к-рый состоит в следующем. Пусть В_k, 0 ∈ B_k (k = 1, 2), - односвязная конечная область в z_k-плоскости, имеющая более одной гранияной точки, и пусть L(r_k, В_k), 0<r<1, - линия уровня функции Грина для B_k, т. е. образ окружности С(r)= {ζ : |ζ| = r} при однолистном конформном отображении круга {ζ : |ζ| < 1} на область В_k, оставляющем неподвижным начало. Пусть далее функция f(z₁), f(0) = 0, осуществляет однолистное конформное отображение области B₁ в область B₂. Тогда: 1) любой точке z⁰₁, лежащей на L(r, B₁), соответствует точка, находящаяся либо на линии уровня L(r, В₂) (это возможно лишь, если f(В₁) = В₂), либо внутри нее; 2) |f'(0)| ≤ |g'(0)|, где g(z₁), g(0) = 0, однолистное конформное отображение B₁ на B₂ (равенство имеет место только в случае f (В₁) = В₂). Принцип Линделёфа выводится из теоремы Римана о конформном изоморфизме областей и из леммы Шварца. Более тонкие построения позволяют находить поточечные отклонения отображающих функций, вызванные заданной деформацией отображаемых областей.

Основной количественный В. п., полученный М. А. Лаврентьевым [1] (см. также [2]), состоит в следующем. Пусть В₁ , 0 ∈ B₁, - односвязная конечная область с аналитич. границей. Пусть имеется семейство областей B₁(t), 0 ∈ B₁(t), 0 ≤ t ≤ T, Т > 0, B₁(0) ≡ B₁, с жордановыми границами Г₁(t) = {z₁ : z₁ = Ω (λ, t)}, 0 ≤ λ ≤ 2π, Ω(0, t) = Ω(2π, t), где Ω(λ, t) равномерно относительно λ дифференцируема по t при t = 0, и пусть F (z₁, t), F(0, t) = 0, F'_z1(0, t) > 0, - функция, однолистно и конформно отображающая B₁(t) на круг B₂ = {z₂: |z₂| < 1}, а Ф (z₂, t) -обратная к F (z₁, t) функция при фиксированном t.

Тогда

F(z₁, t) = F(z₁, 0) - tK(F(z₁, 0)) + γ₁(z₁, t), Ф(z₂, t) = Ф(z₂, 0) + tФ'_z2(z₂, 0) K(z₂) + γ₂(z₂, t),

где

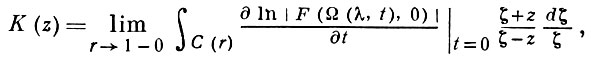
и 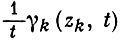равномерно внутри B₂ (k = 1, 2) стремится к нулю при t → 0. В [3] дано распространение этого результата на двусвязные области. При дальнейших ограничениях на области B₁(t) удается получить равномерные в замкнутой области оценки остаточных членов в разложении отображающей функции по параметрам, характеризующим деформацию границ рассматриваемых областей (см. [4]).

Лит.: [1] Лаврентьев М. А., «Тр. Физ.-матем. ин-та АН СССР», 1934, т. 5, с. 159-246; [2] Куфарев П. П., «Матем. сб.», 1943, т. 13(55), № 1, с. 87-118; [3] Александров И. А., «Сиб. матем. ж.», 1963, т. 4, № 5, с. 961 - 76; [4] Лаврентьев М. А., Шабат Б. В., Методы теории функций комплексного переменного, 3 изд., М., 1965.

И. А. Александров.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.