ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ

ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ; численные методы - раздел вычислительной математики, посвященный методам отыскания экстремальных значений функционалов.

Численные методы В. и. принято разделять на два больших класса: непрямые и прямые методы. Непрямые методы основаны на использовании необходимых условий оптимальности (см. Вариационное исчисление, Эйлера уравнение, Вейерштрасса условия, Трансверсальности условие, Понтрягина принцип максимума), с помощью к-рых исходная вариационная задача сводится к краевой задаче. Поэтому вычислительные достоинства и недостатки непрямых методов полностью определяются свойствами соответствующей краевой задачи. Прямые методы ориентированы на непосредственное отыскание экстремума функционала. Используемые при этом методы оптимизации являются развитием идей математич. программирования.

Разделение численных методов В. и. на прямые и непрямые весьма условно. Нек-рые алгоритмы используют элементы обоих подходов. Кроме того, существуют методы, к-рые непосредственно не относятся к двум выделенным классам. Например, методы, основанные на достаточных условиях оптимальности, образуют самостоятельную группу.

Первые численные методы В. и. появились в работах Л. Эйлера (L. Euler). Однако наибольшее развитие они получили с 50-х гг. 20 в. в результате распространения вычислительной техники и открывшейся в связи с этим возможностью решения сложных технич. задач. При этом разработка численных методов В. и. шла в основном применительно к задачам теории оптимального управления - наиболее важного для практич. приложений раздела В. и. (см. Оптимального управления математическая теория).

Непрямые методы. С появлением принципа максимума Понтрягина (1956) сведение вариационных задач к краевым стало особенно популярным.

Пусть в задаче оптимального управления требуется найти траекторию х(t) и управление u(t), доставляющие минимум функционалу

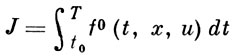
(1)

при дифференциальных связях:

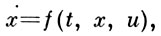
(2)

граничных условиях:

x(t₀) = x₀, (3)

х(Т) = х_T (4)

и ограничениях на управление:

u ∈ U, (5)

где х = (x₁, ..., x_n), u = (u₁, ..., u_n) - векторы фазовых координат и управлений, f = (f₁, ..., f_n), U -замкнутое множество m-мерного пространства, t -независимое переменное (время).

Согласно принципу максимума Понтрягина, оптимальное управление u(t) должно при каждом t доставлять абсолютный максимум Гамильтона функции

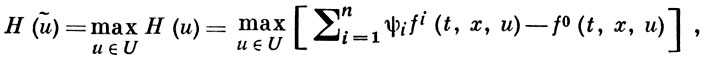
(6)

где ψ = (ψ₁, ..., ψ_n) определяется системой уравнений

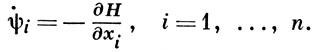
(7)

Из условия (6) находится управление u(t, х, ψ) и подставляется в (2) и (7). В результате получается замкнутая краевая задача для системы 2n дифференциальных уравнений (2) и (7) с 2n граничными условиями (3) и (4).

Наиболее распространенной схемой численного решения этой краевой задачи является схема, использующая метод Ньютона с дроблением шага (см. [3]). При этом вводится вектор невязки

ψ_i = xⁱ(Т) - хⁱ_T , i = 1, ..., n, (8)

где значение хⁱ(Т) получается из решения задачи Коши для системы (2), (7) с начальными условиями (3) и ψ^j(t₀) = ψ^j0, j = 1, ..., n. Невязки (8) рассматриваются как функции от неизвестных ψ₁₀, ..., ψ_n0, к-рые определяются из системы уравнений

ψ_i(ψ₁₀, ..., ψ_n0) = 0, i = 1, ..., n. (9)

Решение системы (9) проводится Ньютона методом; используемые при этом частные производные

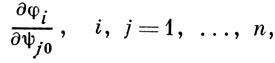
определяются численно по формуле

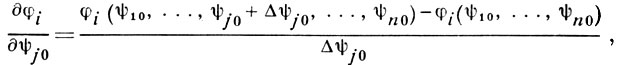
где значения ψ_i(ψ₁₀, ..., ψ_j0 + Δψ_j0, ..., ψ_n0) получаются путем решения задачи Коши для системы (2), (7) с начальными условиями (3) и условиями

ψ_l(t₀) = ψ_l0, ψ_j(t₀) = ψ_j0 + Δψ_j0, l ≠ j. Δψ_j0 - малое приращение величины ψ_j0.

Для определения частных производных известен более точный, но громоздкий метод (см. [4]), в к-ром используется интегрирование системы 2n уравнений в вариациях для системы (2), (7).

Трудности в использовании метода Ньютона связаны, во-первых, с проблемой выбора удачного начального приближения для ψ_j0 и, во-вторых, с неустойчивостью задачи Коши, к-рая особенно сильно проявляется на больших интервалах [t₀, t₁]. Для преодоления первой трудности не существует универсального подхода. Для преодоления неустойчивости задачи Коши имеется ряд приемов (Коши задача; численные методы).

В тех случаях, когда граничные условия и функционал заданы в более общем виде, чем в (3), (4) и (1) [напр., Больца задача с подвижными концами, вариационная задача со свободными (подвижными) концами], к необходимым условиям оптимальности (6), (7) добавляются трансверсальности условия. После исключения входящих в эти условия произвольных постоянных получаются замкнутая краевая задача и отвечающая ей система уравнений типа (9).

Решение системы (9) может отыскиваться любым другим методом, применяемым для решения нелинейных систем.

Специфич. методы разработаны для решения краевых задач частного вида. Так, линейные краевые задачи решаются методом переноса граничных условий (прогонки метод). Этот метод также используется в качестве составного элемента для итеративного решения нелинейных краевых задач (см. [1]).

Эффективность и относительная простота реализации непрямых методов на ЭВМ сделали их весьма распространенным средством для решения задач вариационного исчисления. Однако эти методы не стали универсальными: для некоторых важных классов задач В. и., например, содержащих фазовые ограничения, выписывание необходимых условий оптимальности затруднено и приводит к краевым задачам со сложной структурой. Кроме того, необходимые условия не гарантируют, что найденное решение доставляет относительный экстремум функционалу. Для проверки приходится привлекать достаточные условия оптимальности. Все это ограничивает сферу применения непрямых методов.

Прямые методы. Первый прямой метод был предложен Л. Эйлером для решения простейшей задачи В. и. Этот метод известен под названием метода ломаных Эйлера (или конечно разностного метода Эйлера) и заключается в том, что функционал

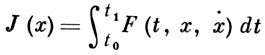
(10)

рассматривается на непрерывных ломаных x(t), удовлетворяющих заданным граничным условиям

x(t₀) = x₀, x(t₁) = x₁ (11)

и состоящих из N прямолинейных отрезков с заданными абсциссами концов. Таким образом, функционал превращается в функцию от ординат вершин этих ломаных, а исходная задача - в задачу минимизации функции многих переменных (см. Эйлера метод).

Из-за сложности подобных задач для ручного счета прямые методы долгое время оставались в стороне от традиционных исследований по В. и. Интерес к ним вновь возрос в нач. 20 в. Были предложены новые способы редукции к задаче об отыскании экстремума функции многих переменных. Наиболее важным из них является Ритца метод, согласно к-рому решение задачи о минимуме (10) при условии (11) разыскивается на классе функций вида

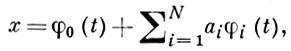
где φ_i(t), i = 0, 1, ..., N - элементы бесконечной полной системы линейно независимых функций, удовлетворяющих граничным условиям

φ₀(t₀) = x₀, φ₀(t₁) = x₁, φ_i(t₀) = φ_i(t₁) = 0, i = 1, 2, ....

Задача сводится к отысканию минимума функции N переменных

J = J (a₁, ..., a_N)

Метод Ритца является достаточно общим. Он применяется для решения вариационных задач математич. физики, заключающихся в минимизации функционала, зависящего от функций многих переменных. Его дальнейшим обобщением для данного класса задач является метод (см. [2]), в к-ром коэффициенты считаются неизвестными функциями одного из независимых переменных (напр., если в задаче две независимые переменные t и τ, то а_i могут задаваться в виде а_i(τ)). Исходный функционал становится зависящим от N функций a_i(τ), к-рые могут определяться с помощью необходимых условий, т. е., в конечном счете, из решения краевой задачи для системы N уравнений Эйлера.

Потребности практики увеличили интерес к неклассич. задачам оптимального управления. Наличие в технич. задачах сложных ограничений на фазовые координаты и управляющие функции, разрывность правых частей дифференциальных уравнений, возможность существования особых и скользящих оптимальных режимов и т. д. - все это потребовало разработки новых разновидностей прямых методов. Наибольшее распространение получили методы, использующие идеи спуска в пространстве управлений и идеи последовательного анализа вариантов (типа динамического программирования).

Методы спуска в пространстве управлений основаны на получении последовательности управлений u_k ∈ U вида

u_k+1(t) = u_k(t) + δu_k(t), (12)

к-рой соответствует монотонно убывающая последовательность значений функционала. Пусть, напр., ищется минимум функционала

J = F(x(T)) (13)

при условиях (2), (3) и (5) (U - выпуклое и односвязное множество). Отыскание δu_k(t) производится следующим образом. С помощью уравнений в вариациях для (2) и сопряженной системы (7) с условиями на правом конце

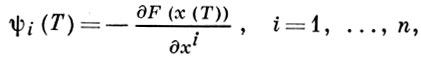
линейная часть приращения функционала (13) от вариации δu представляется в виде

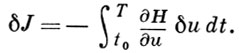
Для уменьшения функционала (13) следует на каждой итерации выбирать приращение

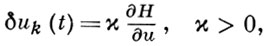
где величина ∂Н/∂u вычисляется на управлении u_k(t) и соответствующей ему траектории x_k(t). Законность линеаризации, а следовательно, и уменьшение функционала (13) обеспечиваются выбором достаточно малой величины א. Процесс спуска (12) начинается с нек-рого u₀(t) и заканчивается, когда на нек-рой итерации |δJ| становится меньше нек-рого заданного ε. Для описанного случая свободного правого конца алгоритм получается наиболее простым (см. [5], [6], [7]). Весьма эффективным для решения задач со свободным концом является метод (см. [8]), к-рый не использует линеаризации исходной задачи. В случае, когда граничные условия заданы и на правом конце, все эти алгоритмы существенно усложняются. Для учета граничных условий в [5] привлекается процедура проектирования градиента, а в [6] вводится штраф за невыполнение граничных условий, т. е. вместо (13) рассматривается функционал

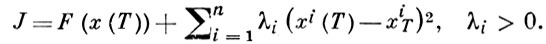
(14)

К градиентным методам примыкает метод [9], в к-ром приращение управления определяется из решения вспомогательной задачи линейного программирования.

Большая группа прямых методов численного решения задач оптимального управления основана на идеях последовательного анализа вариантов (см. [10], [11], [12]). Важным достоинством этих методов является то, что с их помощью удается решать задачи с фазовыми ограничениями вида

x ∈ G, (15)

где G - замкнутое множество n-мерного пространства. Их основной недостаток - существенное возрастание трудностей с увеличением размерности пространства. Эти методы используют редукцию исходной задачи к задаче нелинейного программирования специального вида. Распространены два способа такой редукции. Согласно первому способу в конечном итоге получается задача минимизации функции, зависящей только от управлений, заданных в точках дискретной сетки на оси (см. [13]). Во втором способе (см. [12]) управление исключается и задача сводится к минимизации функции вида

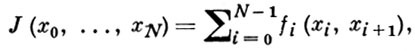
(16)

где х_i - значение вектора х в точке t_i, i = 0, 1, ..., N, при ограничениях

x_i ∈ G_i, (17)

к-рые получаются из ограничений (3), (4), (15). Для пояснения схемы решения задачи минимизации (16) при условиях (17) удобно использовать следующую геометрич. интерпретацию. Каждой совокупности векторов {х₀, х₁, ..., x_N} ставится в соответствие ломаная (см. рис.),

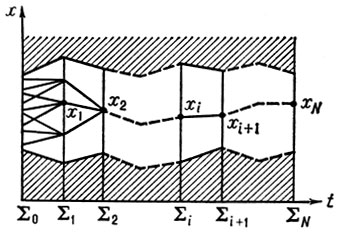
к-рая проходит через точки х₀, ..., x_N, лежащие в гиперплоскостях Σ_i, задаваемых уравнениями t=t_i. Длина этой ломаной J(х₀, ..., x_N) складывается из длин f_i(х_i, х_i+1) отдельных звеньев. Область допустимых значений х_i задается (17) и эта область отделяется от запретной нек-рой ломаной (на рис. запретная область заштрихована). Задача состоит в отыскании ломаной наименьшей длины, лежащей в допустимой области и соединяющей гиперплоскости Σ₀ и Σ_N. Алгоритм решения задачи представляет собой многошаговый процесс, на каждом шаге i к-рого отметается нек-рое множество вариантов Ω_i, заведомо не содержащее оптимальной ломаной. На нулевом шаге определяется функция

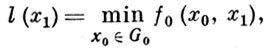
Здесь

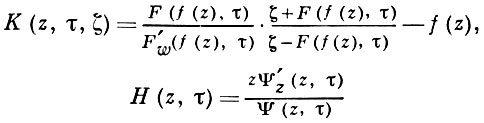
и γ(λ, E) - голоморфная в E функция, предел отношения к-рой к λ при λ → 0 (λ > 0) равномерно стремится к нулю внутри Е.

Использование в процессе исследования экстремальных задач на классе S специальной (упомянутой выше) вариации и уравнения Лёвнера

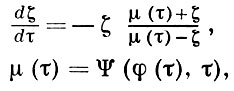
к-рому удовлетворяет функция F(w, τ) при условии F(f(z), 0) = z, обычно позволяет получать для функции, присоединенной к экстремальной, два уравнения. Несмотря на содержащиеся в них постоянные, выражаемые через значения экстремальной функции, дальнейшее исследование этих уравнений в большом числе случаев привело к полному решению рассмотренных задач, в частности к решению задачи об области значений функционала, аналитически зависящего от функции, ее производной и сопряженных им значений на классе S. Метод был предложен П. П. Куфаревым [1] (о дальнейшем его развитии и применениях см. [2] - [5]).

Лит.: [1] Куфарев П. П., «Докл. АН СССР», 1954, т. 97, № 3, с. 391-93; [2] Александров И. А., «Уч. зап. Томск. ун-та», 1958, т. 32, с. 41-57; [3] его же, «Сиб. матем. ж.», 1963, т. 4, № 1, с. 17-31; [4] Редьков М. И., «Докл. АН СССР», 1960, т. 133, № 2, с. 284-87; [5] его же, «Изв. вузов. Математика», 1962, т. 29, с. 134-42.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.