ВАРИАЦИОННАЯ ЗАДАЧА

ВАРИАЦИОННАЯ ЗАДАЧА - 1) В. з. с закрепленными концами - задача вариационного исчисления, в к-рой концы кривой, доставляющей экстремум, зафиксированы. Напр., в простейшей задаче вариационного исчисления

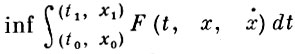
с закрепленными концами заданы начальная и конечная точки x(t₀) = x₀, x(t₁) = x₁, через к-рые должна проходить искомая кривая x(t). Учитывая, что общее решение Эйлера уравнения простейшей задачи зависит от двух произвольных постоянных x = x(t, c₁, с₂), кривая, доставляющая экстремум, ищется среди решений соответствующей краевой задачи. При этом может оказаться, что краевая задача имеет единственное решение, неединственное или не имеет решения.

2) В. з. со свободными (подвижными) концами - задача вариационного исчисления, в к-рой концы кривой, доставляющей экстремум, могут перемещаться вдоль заданных многообразий. Напр., если в Больца задаче число граничных условий, к-рым должна удовлетворять искомая кривая х = (x₁(t), ..., x_n(t)) строго меньше 2n+2:

ψ_μ (t₁, x(t₁), t₂, x(t₂)) = 0, μ = 1, ..., p < 2n + 2, (*)

то концы кривой могут смещаться вдоль (2n + 2 - р)-мерного многообразия (*). В случае, когда граничные условия (*) заданы в виде

ψ_ρ (t₁, x(t₁)) = 0, ψ_σ (t₂, x(t₂)), ρ = 1, ..., r, σ = 1, ..., q,

и n+1-r > 0 или n+1-q > 0, концы кривой x(t) могут смещаться по соответствующим многообразиям размерностей n+1-r и n+1-q. На концах кривой, доставляющей экстремум, должны выполняться трансверсальности условия, к-рые в совокупности с условиями (*) позволяют получить замкнутую систему соотношения, приводящую к нек-рой краевой задаче. Из решения этой краевой задачи определяются произвольные постоянные, входящие в общий интеграл уравнения Эйлера.

Качественным отличием В. з. от задачи на экстремум функции многих переменных является то, что объектом поиска в В. з. является не точка в конечномерном пространстве, а функция (или точка в бесконечномерном пространстве).

И. Б. Вапнярский.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.