ÂÀÍÄÅÐÌÎÍÄÀ ÎÏÐÅÄÅËÈÒÅËÜ

ÂÀÍÄÅÐÌÎÍÄÀ ÎÏÐÅÄÅËÈÒÅËÜ - îïðåäåëèòåëü ïîðÿäêà n âèäà:

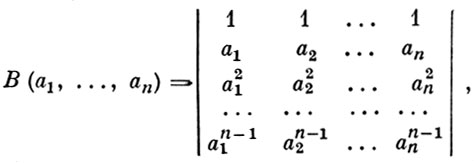
ãäå a₁, ..., a_n ýëåìåíòû íåê-ðîãî êîììóòàòèâíîãî êîëüöà. Ïðè ëþáîì n ≥ 2

B(a₁, ..., a_n) = ∏_1≤j<i≤n (a_i - a_j)

Äëÿ êîëåö áåç äåëèòåëåé íóëÿ èìååò ìåñòî îñíîâíîå ñâîéñòâî Â. î.: B(a₁, ..., a_n) = 0 òîãäà è òîëüêî òîãäà, êîãäà ñðåäè ýëåìåíòîâ a₁, ..., a_n íå âñå ýëåìåíòû ðàçëè÷íû. Â. î. áûë ðàññìîòðåí âïåðâûå À. Ò. Âàíäåðìîíäîì äëÿ ñëó÷àÿ n = 3 (ñì. [1]), çàòåì Î. Êîøè (1815, ñì. [2]).

Ëèò.: [1] Vandårmîndå À. Ò., â êí.: Histoire de l'Académie royale des sciences, année 1771, P., 1774, p. 365-416; année 1772, pt 2, P., 1776, p. 516-32; [2] Ñauñhó A., Oeuvres, ser. 2, t. 1, P., 1905, p. 91-169.

Â. H. Ðåìåñëåííèêîâ.

Èñòî÷íèêè:

1. Ìàòåìàòè÷åñêàÿ Ýíöèêëîïåäèÿ. Ò. 1 (À - Ã). Ðåä. êîëëåãèÿ: È. Ì. Âèíîãðàäîâ (ãëàâ ðåä) [è äð.] - Ì., «Ñîâåòñêàÿ Ýíöèêëîïåäèÿ», 1977, 1152 ñòá. ñ èëë.