ВАЛЛЕ ПУССЕНА ТЕОРЕМА

ВАЛЛЕ ПУССЕНА ТЕОРЕМА - 1) В. П. т. о распределении простых чисел: пусть π(х) - число простых чисел, меньших х; тогда при х≤1 выполняется равенство

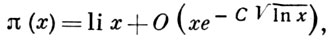
где С - нек-рая положительная постоянная, a li х -интегральный логарифм х. Из В. П. т. следует справедливость гипотезы Гаусса о распределении простых чисел, т. е. при х → +∞

li х ~ x/ln x.

Установлена Ш. Валле Пуссеном [1]. См. Распределение простых чисел.

Лит.: [1] La Vallée Poussin Ch. J., "Аnn. Soc. sci. Bruxelles", 1899, t. 20, p. 183-256; [2] eго же, "Меm. couronnes Acad. sci. de Belgique", 1899-1900, t. 59, № 1; [3] Пpaxap К., Распределение простых чисел, пер. с англ., М., 1967.

С. М. Воронин.

2) В. П. т. об альтернансе: если последовательность точек {х_i}, i = 0, 1, ..., n + 1 замкнутого множества Q ∈ [a, b] образует альтернанс, то для наилучшего приближения функции f(x) полиномами вида

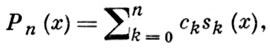
где {s_k(x)}ⁿ₀ - система Чебышева, верна оценка:

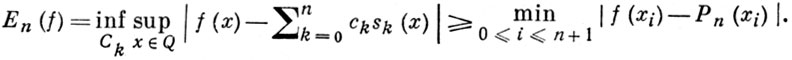
Установлена Ш. Валле Пуссеном [1].

По Чебышева теореме равенство достигается тогда и только тогда, когда Р_n(х) - полином наилучшего приближения. Имеются аналоги этой теоремы для произвольных банаховых пространств [2]. Применяется в численных методах построения полиномов наилучшего приближения.

Лит.: [1] Lа Vаlléе Poussin Сh. J., Sur les роlynômes d'approximation et la représentation approchée d'un angle, «Bull. Acad. de Belgique», 1910, t. 12, p. 808-45; [2] Гapкaви А. Л., в сб.: Итоги науки. Математический анализ. 1967, М., 1969, с. 75-132.

Ю. Н. Субботин.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.