ВАЛЛЕ ПУССЕНА МНОГОТОЧЕЧНАЯ ЗАДАЧА

ВАЛЛЕ ПУССЕНА МНОГОТОЧЕЧНАЯ ЗАДАЧА - задача отыскания решения обыкновенного нелинейного дифференциального уравнения n-го порядка

y⁽ⁿ⁾ = f (x, y, y', ..., y^(n-1)) (1)

или линейного уравнения

y⁽ⁿ⁾ + p₁(x) y^(n-1) + ... + p_n(x)y = 0, (2)

где х ∈ [а, b], |y^(s)| < +∞ , s = 0, 1, . . ., n-1, при условиях

у(х_i) = с_i, i = 1, 2, ..., n; х ∈ [а, b]. (3)

Ш. Валле Пуссен [1] доказал, что если p_k (х) ∈ С_[a,b] k = 1, 2, ..., n, и выполняется неравенство

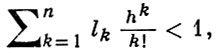
(4)

где l_k ≥ |p_k(x)|, k = 1, 2, . . ., n, х ∈ [а, b], h = b - a, то существует единственное решение задачи (2), (3). Им же было доказано, что если f(x, u₁, ..., u_n) непрерывна по всем своим аргументам и удовлетворяет условиям Липшица с константами l_k по переменным u_n+1-k, k = 1, 2, ..., n, то при выполнении неравенства (4) может существовать лишь одно решение задачи (1), (3).

Исследования по В. П. м. з. проводятся в следующих направлениях: улучшение оценки числа h с помощью изменения коэффициентов в (4); расширение класса функций P_k(x), k = l, 2, ..., n, или f(x, u₁, ..., u_n); обобщение условий (3). Основная проблема (1977) - доказательство существования и единственности решения. Для задачи (2), (3) это свойство равносильно следующему: любое нетривиальное решение уравнения (2) имеет не более n - 1 нулей на [а, b] [неосцилляция (или неколеблемость) решений, или разъединенность нулей].

Лит. : [1]La Vallée Poussin Ch. J., «J. math. pures et appl.», 1929, сер. 9, t. 8, № 1, p. 125-44; [2] Сансоне Дж., Обыкновенные дифференциальные уравнения, пер. с итал., т. 1, М., 1953.

Л. Н. Ешуков.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.