БЮФФОНА ЗАДАЧА

Расстановка ударений: БЮФФО`НА ЗАДА`ЧА

БЮФФОНА ЗАДАЧА об игле - классическая задача теории геометрических вероятностей, по праву считающаяся исходным пунктом развития этой теории. Впервые была отмечена Ж. Бюффоном в 1733 и воспроизведена вместе с решением в [1]. Ж. Бюффон рассматривал следующую ситуацию: на плоскость, разграфленную параллельными прямыми, отстоящими друг от друга на расстоянии а, наудачу бросается игла длиною 2r(2r < а). Какова вероятность того, что игла пересечет одну из проведенных параллелей? Очевидно, что положение иглы определяется расстоянием х от ее центра до ближайшей прямой линии и острым углом θ, составленным иглой с перпендикуляром к этой линии. Величина х лежит между нулем и а/2, а θ - между нулем и π /2. Предполагается, что точка (х, θ) распределена равномерно в соответствующем прямоугольнике (это равносильно тому, что случайные величины х и θ независимы и равномерно распределены на (0, а/2) и (0, π /2)). Тогда искомая вероятность определяется как отношение площадей, соответствующих благоприятствующим и всем возможным исходам, и равна

(*)

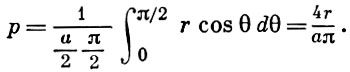
В свое время Б. з. послужила основой для экспериментальной проверки Бернулли теоремы. Действительно, если игла бросается n раз и в m случаях игла пересекает одну из линий, то частота m/n при больших n по теореме Бернулли должна быть близка к вероятности (*). Это соображение было использовано многими исследователями для определения числа л методом случайных испытаний (см. [1], [2]). Ж. Бюффон рассматривал и другие сходные задачи, в частности задачу о вероятности пересечения иглой линий, принадлежащих двум взаимно перпендикулярным системам, к-рые разбивают плоскость на прямоугольники со сторонами а и b, соответственно. Ответ Ж. Бюффона к этой задаче неверен. Правильный ответ:

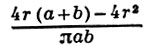
был указан П. Лапласом (P. Laplace) в 1812.

Лит. : [1] Button G., Essai d'arithmetique morale. Supplementа «l'Histoire Naturelle», v. 4, 1777; [2] Uspenskу J. V., Introduction to mathematical Probability, N. Y. - L., 1937; [3] Кендалл M., Моран П., Геометрические вероятности, пер. с англ., М., 1972.

А. В. Прохоров.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.