БЮРМАНА-ЛАГРАНЖА РЯД

Расстановка ударений: БЮ`РМАНА-ЛАГРА`НЖА РЯ`Д

БЮРМАНА-ЛАГРАНЖА РЯД, ряд Лагранжа, - степенной ряд, полностью решающий задачу локального обращения голоморфных функций. Именно, пусть функция w = g(z) комплексного переменного z регулярна в окрестности точки z = a, причем g(a) = b и g'(а) ≠ 0. Тогда в нек-рой окрестности точки w = b плоскости w определена регулярная функция z = h(w), обратная по отношению к g(z) и такая, что h(b) = a; при этом, если f(z) - любая регулярная в окрестности точки z = a функция, то сложная функция F(w) = f[h(w)] разлагается в окрестности точки w = 6 в ряд Бюрмана-Лагранжа

(*)

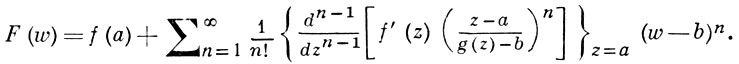
Случай непосредственного обращения функции w = g(z) получается при f(z) ≡ z.

Разложение (*) вытекает из теоремы Бюрмана [1]: при указанных выше предположениях относительно голоморфных функций g(z) и f(z) последняя в нек-рой области на плоскости z, содержащей точку а, может быть представлена в виде:

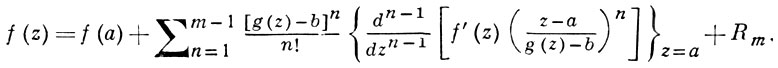
где

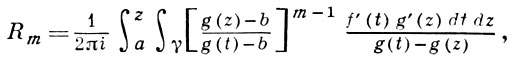
γ - контур на плоскости t, содержащий внутри точки а и z и такой, что если ζ - какая-либо точка внутри γ, то уравнение g(t) = g(ζ) не имеет ни на γ, ни внутри γ иных корней, кроме простого корня t = ζ.

Разложение (*) для случая b = 0 было получено Ж. Лагранжем [2].

В случае, когда производная g'(t) имеет в точке z = a нуль порядка r - 1, Б.-Л. р. для многозначной обратной функции допускает следующее обобщение (см. [3]):

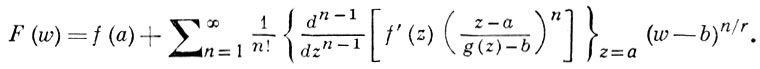
Другое обобщение (см., напр., [4]) относится к функциям g(z), регулярным в кольце; оно приводит вместо ряда (*) к ряду по положительным и отрицательным степеням разности w - b.

Лит. : [1] Burmann H., «Мет. de l'Inst. national des sci. et arts. Sci. Math, et Phys. », P., 1799, t. 2, p. 13-17; [2] Lagrange J. L., «Mem. de l'Académie royale des sci. et belles-lettres de Berlin», 1770, t. 24; uvres, t. 2, P., 1868, p. 581-652; [3] Гуpвиц А., Курант Р., Теория функций, пер. с нем., М., 1968, ч. 1, гл. 8; [4] Уиттекер Э. Т., Ватсон Дж. Н., Курс современного анализа, пер. с англ., 2 изд., т. 1, М., 1962; [5] Маркушевич А. И., Теория аналитических функций, 2 изд., т. 1, М., 1967.

Е. Д. Соломенцев.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.