БЭРРИ-ЭССЕЕНА НЕРАВЕНСТВО

Расстановка ударений: БЭ`РРИ-ЭССЕ`ЕНА НЕРА`ВЕНСТВО

БЭРРИ-ЭССЕЕНА НЕРАВЕНСТВО - неравенство, дающее оценку отклонения функции распределения суммы независимых случайных величин от нормальной функции распределения. Пусть X₁, ..., X_n - независимые одинаково распределенные случайные величины такие, что

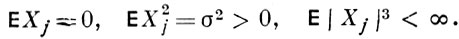
Пусть

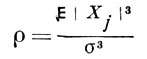
и

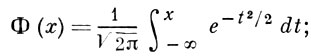
тогда для любого n

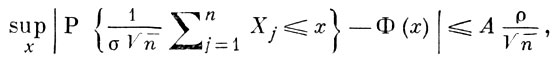
где А - абсолютная положительная постоянная. Этот результат был получен А. Бэрри [1] и независимо от него К.-Г. Эссееном [2].

Лит. : [1] Berry А. «Trans. Amer. Math. Soc. », 1941, v. 49, № 1, p. 122-36; [2] Esseen C.-G., «Ark. Mat., Astr. och Fysik», 1942, Bd 28A, № 9, p. 1-19; [3] Петров В. В., Суммы независимых случайных величин, М., 1972.

В. В. Петров.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.