БЭРА УМНОЖЕНИЕ

Расстановка ударений: БЭ`РА УМНОЖЕ`НИЕ

БЭРА УМНОЖЕНИЕ - бинарная операция на множестве классов эквивалентных расширений модулей; предложена Р. Бэром [1]. Пусть А и В - произвольные модули. Расширением А с ядром В наз. точная последовательность:

O → B → X → A → O. (1)

Расширение (1) наз. эквивалентным расширению

O → B → X₁ → A → O,

если существует гомоморфизм α : X → X₁ включаемый в коммутативную диаграмму:

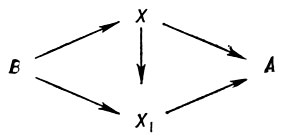
Множество классов эквивалентных расширений обозначается Ext (А, В). Б. у. на Ext (А, В) индуцируется следующим образом определенной операцией произведения расширений. Пусть

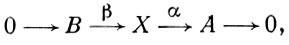
(2)

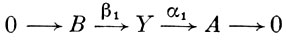
(3)

два расширения. В прямой сумме X⊕ Y выбираются подмодули

С = {(х, у) | α (х) = α (у)}

и

D = {(- x, у) | х = β (b), y = β₁ (b)}.

Ясно, что D ⊂ C, так что определен фактормодуль Z = С/D. Произведением Бэра расширений (2) и (3) наз. расширение

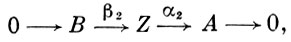
где

β₂ (b) = [β (b), 0] = [0, β '(b)];

а

α₂ [x, у] = α (х) = α₁ (у).

Лит. : [1] Ваеr R., «Math. Z. », 1934, Bd 38, S. 374-416; [2] Кapтан А., Эйленберг С. Гомологическая алгебра, пер. с англ., М., 1960.

В. Е. Говоров.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.