БУТТА ЛЕМНИСКАТА

Расстановка ударений: БУ`ТТА ЛЕМНИСКА`ТА

БУТТА ЛЕМНИСКАТА - плоская алгебраич. кривая 4-го порядка, уравнение к-рой в декартовых прямоугольных координатах имеет вид:

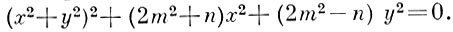
Если |n| < 2m², то Б. л. наз. эллиптической Б. л. (имеет изолированную особую точку О, см. рис. 1, где 0 < n < 2m²). Если |n| > 2m², то Б. л. наз. гиперболической Б. л. (имеет в начале координат узловую точку, см. рис. 2, где n > 2m² . В полярных координатах уравнение эллиптич. Б. л. имеет вид:

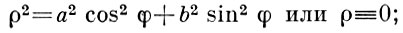
если n > 2m², то уравнение гиперболической Б. л. имеет вид:

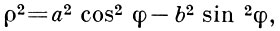
если n < - 2m² :

ρ²= -a² cos² φ + b² sin² φ

(a² = |2m² + n|, b² = |2m² - n|).

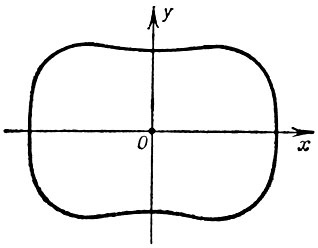
Рис. 1.

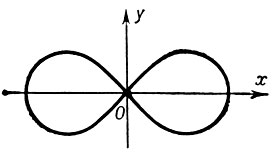
Рис. 2.

Длина дуги Б. л. выражается через эллиптич. интегралы. Площадь, ограничиваемая эллиптич. Б. л. :

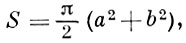
гиперболич. Б. л. :

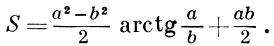
Б. л. - частный случай Персея кривой. Б. л. названа по имени Дж. Бута [1].

Лит. : [1] Booth J., A treatise on some new geometrical methods, v. 1-2, L., 1873-77; [2] Савeлов А. А., Плоские кривые, M., 1960, с. 144-46.

Д. Д. Соколов.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.