БУЛЕВЫХ ФУНКЦИЙ НОРМАЛЬНЫЕ ФОРМЫ

Расстановка ударений: БУ`ЛЕВЫХ ФУ`НКЦИЙ НОРМА`ЛЬНЫЕ ФО`РМЫ

БУЛЕВЫХ ФУНКЦИИ НОРМАЛЬНЫЕ ФОРМЫ - формулы специального вида, реализующие булевы функции. Различают дизъюнктивные нормальные формы (д. н. ф. ; см. Булевых функций минимизация) и конъюнктивные нормальные формы (к. н. ф.). Произведение x_i1^σ₁ x_i2^σ₂ ...x_ik^σ_k, где х^σ = х при σ = 1 и х^σ = х¯ при σ = 0, наз. элементарной конъюнкцией ранга k, если все переменные в нем различны; 1 считается элементарной конъюнкцией нулевого ранга. Логическая сумма x_j1^σ₁ ∨ x_j2^σ₂ ∨... ∨ x_jk^σ_k наз. элементарной дизъюнкцией ранга r, если все переменные в ней различны; 0 считается элементарной дизъюнкцией нулевого ранга.

Формула 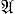₁ ∨... ∨ 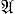_l, где 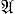₁, ..., 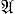_l - различные элементарные конъюнкции рангов r₁, ..., r_l соответственно, наз. д. н. ф., а число 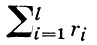- сложностью этой д. н. ф. ; формула ₁ ..._t, где ₁, ..., _t - различные элементарные дизъюнкции рангов ρ₁, ..., ρ_t соответственно, наз. к. н. ф., а число 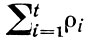- сложностью этой к. н. ф. Всякая булева функция, отличная от тождественного нуля, может быть задана д. н. ф. и, вообще говоря, неоднозначно. Аналогичный факт имеет место для к. н. ф. и функций, не равных тождественно единице.

По таблице, задающей булеву функцию f(x₁, ..., x_n), легко строится совершенная д. н. ф. 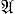₁ ∨... ∨ 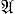_s, где 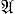_i = x₁^σ_i1 ∨ x₂^σ_i2 ∨... ∨ x_n^σ_in, i = 1, 2, ..., s, и наборы σ_i1, σ_i2, ..., σ_in таковы, что f(σ_i1, σ_i2, ..., σ_in) = 1. Совершенная д. н. ф., реализующая булеву функцию f, строится однозначно. Аналогично определяется совершенная к. н. ф.

Так как «почти все» булевы функции имеют число единичных наборов в пределах от 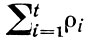до 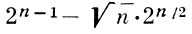, то асимптотич. сложность совершенной д. н. ф. для «почти всех» булевых функций равна n ⋅ 2^{n - 1} . Максимальная сложность совершенной д. н. ф. для функций от n переменных достигается для функций, равных 0, в одной точке. Она равна n ⋅ (2ⁿ - 1).

Основной задачей в теории Б. ф. н. ф. является задача минимизации булевых функций, т. е. построение для произвольной булевой функции к. н. ф. или д. н. ф. минимальной сложности - минимальной к. н. ф. или д. н. ф. (см. Булевых функций минимизация, Алгоритм локальный). При этом, в силу принципа двойственности, достаточно рассматривать только д. н. ф. В связи с задачей минимизации булевых функций рассматриваются также д. н. ф. сокращенная, тупиковые, кратчайшие и минимальные. Важной задачей теории д. н. ф. является отыскание их числовых характеристик, а также характеристик, связывающих различные типы д. н. ф. одной функции.

Сокращенная д. н. ф. строится по булевой функции однозначно с помощью достаточно простых алгоритмов. Ее важнейшим свойством является то, что всякая минимальная д. н. ф. функции и хотя бы одна кратчайшая получаются из сокращенной д. н. ф. удалением нек-рых элементарных конъюнкций. Поэтому многие алгоритмы минимизации используют сокращенные д. н. ф. качестве исходного задания булевой функции. В связи с этим большой интерес представляет определение сложности сокращенных д. н. ф. для «почти всех» функций и выяснение абсолютного максимума этой сложности. Если S_f (n) - число элементарных конъюнкций в сокращенной д. н. ф. булевой функции f(x₁, ..., x_n) и

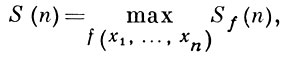
то имеют место следующие оценки:

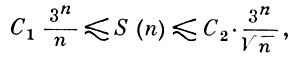
и для «почти всех» булевых функций

Из этих результатов и оценок сложности совершенной д. н. ф. видно, что сложность сокращенной д. н. ф. существенно больше сложности совершенной д. н. ф. как в «типичном», так и в «рекордном» случаях. В отличие от совершенной и сокращенной д. н. ф., у одной булевой функции может быть много тупиковых и минимальных д. н. ф. Пусть t_f (n) - число тупиковых д. н. ф., m_f (n) - число минимальных д. н. ф. булевой функции f(x₁, ..., x_n),

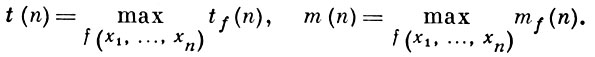
Имеют место следующие оценки:

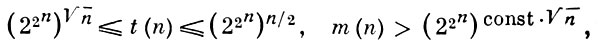
и для «почти всех» булевых функций

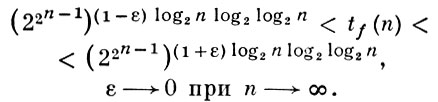
Верхняя оценка для m(n) и оценка m_f (n) для «почти всех» функций, отличных от тривиальных, пока (1977) не найдены. Большой интерес в задачах минимизации булевых функций представляют оценки сложности тупиковых д. н. ф. и минимальных д. н. ф. Пусть λ_f^T (n) - число элементарных конъюнкций в тупиковой д. н. ф. Т функции f(x₁, ..., x_n); l_f (n) - число элементарных конъюнкций в кратчайших д. н. ф. функции f(x₁, ..., x_n),

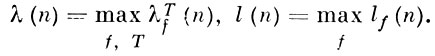
Имеют место следующие оценки:

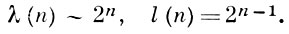
У «почти всех» булевых функций f(x₁, ..., x_n) для почти всех тупиковых д. н. ф. Т:

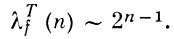
Для «почти всех» булевых функций f(x₁, ..., x_n)

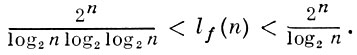
Эти оценки показывают, что кратчайшие (а также минимальные) д. н. ф. составляют у «почти всех» булевых функций малую долю от числа тупиковых д. н. ф. Существуют также оценки относительной сложности тупиковых д. н. ф. и кратчайших д. н. ф. булевых функций. Пусть λ_f (n) - максимальное число элементарных конъюнкций в тупиковой д. н. ф. функции f(x₁, ..., x_n). Для «почти всех» булевых функций

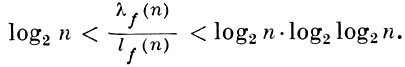
Максимальное значение отношения λ_f (n)/l_f (n) оценивается снизу величиной 2^{n(1 - ε)}, ε - → 0 при n → ∞. Получены также оценки для величины y(f), наз. разбросом булевой функции f(x₁, ..., x_n). Здесь

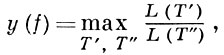
где Т' и Т'' - произвольные тупиковые д. н. ф., реализующие f(x₁, ..., x_n), а L(Т) - число букв в тупиковой д. н. ф. Т. Построены примеры булевых функций, у к-рых у(f)̥ 2^{n(1 - o(1))} ; установлено, однако, что для «почти всех» булевых функций

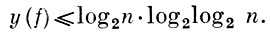
Приведенные выше оценки позволяют получить полное представление о тех трудностях, к-рые возникают при минимизации булевых функций по схеме: совершенная д. н. ф. - сокращенная д. н. ф. - тупиковая д. н. ф. - минимальная д. н. ф.

Лит. : [1] Васильев Ю. Л., «Проблемы кибернетики», 1963, в. 10, с. 5-61; [2] Глаголев В. В., «Проблемы кибернетики», 1967, в. 19, с. 75-94; [3] Коршунов А. Д., «Кибернетика», 1969, т. 6, с. 1-8; [4] Сапоженко А. А., «Матем. заметки», 1968, т. 4, № 6, с. 649-58.

Ю. И. Журавлев.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.