БУЛЕВЫХ ФУНКЦИЙ МИНИМИЗАЦИЯ

Расстановка ударений: БУ`ЛЕВЫХ ФУ`НКЦИЙ МИНИМИЗА`ЦИЯ

БУЛЕВЫХ ФУНКЦИЙ МИНИМИЗАЦИЯ - представление булевых функций нормальными формами (см. Булевых функций нормальные формы), простейшими относительно нек-рой меры сложности. Обычно под сложностью нормальной формы понимается число букв в ней. В этом случае простейшая форма наз. минимальной. Иногда в качестве меры сложности рассматривается число элементарных конъюнкций в дизъюнктивной нормальной форме или число сомножителей в конъюнктивной нормальной форме. В этом случае простейшая форма наз. кратчайшей. В силу двойственности дизъюнктивных и конъюнктивных нормальных форм достаточно рассматривать только дизъюнктивные нормальные формы (д. н. ф.).

Построение кратчайших и минимальных д. н. ф. имеет каждое свою специфику. Множества минимальных и кратчайших д. н. ф. одной и той же функции могут находиться в любых теоретико-множественных соотношениях: содержаться одно в другом, иметь пустое пересечение или непустую симметрическую разность. Если для функции f обозначить через m_f сложность минимальной д. н. ф., через k_f - минимальную сложность кратчайшей д. н. ф., а через l(n) - наибольшее из отношений k_f /m_f по всем функциям от n переменных, то справедливо асимптотич. соотношение:

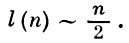
Обычно под задачей Б. ф. м. понимается задача построения их минимальных д. н. ф. Существует тривиальный алгоритм построения всех минимальных д. н. ф. для произвольной булевой функции f(x₁, ..., x_n). Он состоит в просмотре всех д. н. ф. с переменными x₁, ..., x_n и выделении тех из них, к-рые реализуют функцию f и имеют минимальную сложность. Этот алгоритм фактически неприменим уже при небольших n ввиду быстрого роста числа операций. Поэтому было построено большое число других алгоритмов, к-рые, однако, эффективно применимы не ко всем функциям.

Исходным заданием функции в задаче минимизации обычно считают таблицу, совершенную д. н. ф. (см. Булевых функций нормальные формы) или произвольную д. н. ф. На первом этапе от исходного задания осуществляется переход к так наз. сокращенной д. н. ф., к-рая определена для каждой функции однозначно. Существует большое число методов реализации этого перехода. Наиболее универсальный метод состоит в выполнении над д. н. ф. преобразований вида

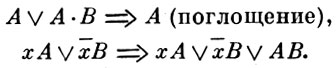
Сокращенная д. н. ф. обладает тем свойством, что любая минимальная д. н. ф. получается из нее удалением нек-рых элементарных конъюнкций. Второй, наиболее трудоемкий, этап состоит в полунении из сокращенной д. н. ф. всех тупиковых д. н. ф., среди к-рых содержатся и все минимальные. На этом этапе обычно используется геометрич. представление булевых функций. Пусть Е_n обозначает множество всех вершин n-мерного единичного куба. Каждой булевой функции f(x₁, ..., x_n) взаимно однозначно соответствует подмножество N_f, N_f ⊆ E_n, таких вершин α̃, где f(α̃) = 1. Пусть - элементарная конъюнкция ранга r, тогда множество N наз. интервалом ранга r, соответствующим элементарной конъюнкции . Говорят, что система интервалов N₁, ..., N_m образует покрытие множества N ⊆ _n, если

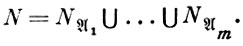
Так как равенства

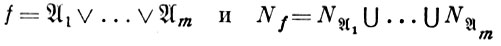
эквивалентны, то задача Б. ф. м. равносильна отысканию покрытий, сумма рангов интервалов к-рых минимальна. Такие покрытия наз. минимальными. Интервал N наз. максимальным для функции f, если N ⊆ N_f и не существует интервала N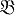 такого, что N ⊂ N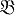 ⊆ N_f . Построение тупиковых д. н. ф. функции f сводится к отысканию таких покрытий множества N_f максимальными интервалами, никакое собственное подмножество к-рых не является покрытием множества N_f . Эти покрытия соответствуют тупиковым д. н. ф. и наз. неприводимыми. Они получаются из покрытий, соответствующих сокращенным д. н. ф., путем удаления нек-рых интервалов.

Выбор минимальных д. н. ф. из всех тупиковых также оказывается весьма трудоемким процессом, поскольку для «почти всех» булевых функций от n аргументов различных тупиковых д. н. ф. не меньше, чем 2²ⁿ . При этом разброс сложностей тупиковых д. н. ф. может быть очень велик, так что выбор случайной тупиковой д. н. ф. вместо минимальной может привести к большой погрешности.

Оценки числа тупиковых д. н. ф. и разброса сложностей показывают, что естественным путем улучшения эффективности алгоритмов минимизации является путь более тонких рассмотрений при удалении элементарной конъюнкции из д. н. ф. Удалять (или, наоборот, закреплять до конца процесса) конъюнкцию следует лишь в том случае, если для нее посредством нек-рой процедуры удается установить, что она не входит ни в одну минимальную д. н. ф. для f (входит во все минимальные д. н. ф. для f). Последний факт устанавливается обычно при помощи анализа конъюнкций, близких к рассматриваемой, т. е. входящих в окрестность этой конъюнкции (см. Алгоритм локальный). При этом разрешается накапливать информацию об элементарных конъюнкциях и использовать ее в дальнейшем анализе. Процедуры указанного вида получили назв. локальных алгоритмов упрощения. Ниже приводятся нек-рые из них. В их описании используется понятие окрестности k-го порядка S_k (, ) элементарной конъюнкции в д. н. ф. ∈ .

Окрестность нулевого порядка S₀ (, ) состоит из одной конъюнкции . Если S_{k - 1} (, ) есть окрестность (k - 1)-го порядка, то окрестность k-го порядка S_k (, ) состоит из всех конъюнкций _j д. н. ф. , удовлетворяющих одному из следующих условий: 1) N_j имеет непустое пересечение хотя бы с одним интервалом, соответствующим конъюнкции из S_{k - 1} (, ); 2) N_j ⊆ ∪^r_{i = 1} N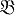_i, где N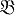_i, i = 1, 2, ..., r, удовлетворяют условию 1).

Алгоритм Куайна. На каждом шаге рассматривается окрестность S₁ (, ) одной из конъюнкций в д. н. ф. . В процессе работы алгоритма для каждой из конъюнкций делается попытка вычислить одно из свойств: Р₁ (, ) -

« входит во все минимальные д. н. ф. », Р₂ (, ) -

« - не входит ни в одну минимальную д. н. ф. ».

Алгоритм работает следующим образом. 1) По очереди для каждой конъюнкции из строится окрестность S(, ) = {, ₁, ..., _m). Проверяется включение: N ⊆ ∪^m_{i = 1} N_i . Если оно не имеет места, то отмечается нек-рым способом как входящая во все минимальные д. н. ф. В этом случае говорят, что входит в ядро д. н. ф. (является ядровой конъюнкцией). 2) Пусть на первом этапе в отмечены конъюнкции 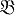₁, ..., 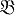_q . Остальные конъюнкции из упорядочиваются, и для каждой такой конъюнкции 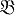проверяется включение N 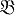⊆ ∪^q_{i = 1} N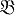_i. Конъюнкции, для к-рых это соотношение выполнено, не входят ни в одну минимальную д. н. ф. ; они удаляются из .

Алгоритм регулярных точек. Этот алгоритм на каждом шаге осматривает окрестность S₂ (, ) конъюнкции в д. н. ф. и удаляет конъюнкции, не входящие ни в одну тупиковую и, следовательно, ни в одну минимальную д. н. ф. В описании алгоритма используется понятие α̃ - пучка в д. н. ф. представляющего собой для рассматриваемой точки α̃ из N множество М (α̃, ) интервалов N_j таких, что _j ∈ , α̃ ∈ N_j . Для конъюнкции из д. н. ф. точка α̃ из N наз. регулярной относительно (, ), если существует точка α̃ ' такая, что α̃ ' ∈ N \N и М(α̃ ', ) ⊆ М(α̃, ). Множество М ⊆ N наз. регулярным относительно (, ), если все его точки регулярны относительно (, ) - Описываемый алгоритм основывается на том, что конъюнкция из сокращенной д. н. ф. функции f не входит ни в одну тупиковую д. н. ф. функции f тогда и только тогда, когда N есть множество, регулярное относительно (, ) - Алгоритм проверяет в нек-ром порядке, являются ли интервалы конъюнкций, входящих в д. н. ф., регулярными множествами, и удаляет те из них, интервалы к-рых регулярны. Свойство интервала N быть регулярным относительно (, ) полностью определяется окрестностью S₂ (, ) и> вообще говоря, не определяется окрестностью S₁ (, )

А - алгоритм. Здесь используется понятие д. н. ф., минимальной относительно д. н. ф. , т. е. такой д. н. ф., к-рая минимальна среди всех д. н. ф., эквивалентных и получающихся из опусканием нек-рых элементарных конъюнкций. Рассматриваются два свойства элементарной конъюнкции в д. н. ф. :

P₁ (, ) - « входит во все д. н. ф., минимальные относительно », и

P₂ (, ) - « не входит ни в одну д. н. ф., минимальную относительно » -

Считается, что Р_i = 1, если свойство Р_i имеет место, и Р_i = 0 в противном случае. Предполагается, что д. н. ф. составлены из конъюнкций с информационными отметками (ω₁, ω₂), где ω_i ∈ {0, 1, Δ }. При этом равенство ω_i = Δ означает, что свойство Р_i не вычислено (i = 1, 2), а равенства ω_i = 1 означают, что Р_i = ω_i (i = 1, 2). Конъюнкция с информационными отметками (ω₁, ω₂) обозначается через ^{ω₁ ω₂} . А - алгоритм вычисляет значения свойств Р₁ и Р₂ для конъюнкций из д. н. ф. используя для этого лишь конъюнкции из окрестности S₂ (, ) и их информационные отметки. Для конъюнкции ранга r из д. н. ф. множество М ⊃ N наз. множеством первого типа относительно (, ), если в д. н. ф. существуют конъюнкции ₁, ..., _m рангов r₁, ..., r_m такие, что M ⊆ ∪^m_{j = 1} N_j и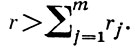

Разностью ₁ \₂ д. н. ф. ₁ и ₂ наз. д. н. ф., состоящая из элементарных конъюнкций, входящих в ₁ и не входящих в ₂ .

До применения A - алгоритма все конъюнкции из рассматриваемой д. н. ф. имеют отметку (Δ, Δ). Если выполнены i шагов и отметку (1, Δ) получили конъюнкции '₁, ..., '_s, а отметку (Δ, 1) - конъюнкции ''₁, ..., ''_t, то (i + 1)-й шаг состоит в следующем. Упорядочивают нек-рым способом конъюнкции из д. и. ф. Если д. н. ф. \(∨^s_{j = 1}'_j ∨ ∨^t_{j = 1}''_j) пустая, то A - алгоритм заканчивает свою работу. В противном случае после упорядочивания к.-л. способом конъюнкций из этой д. н. ф. выделяются первая по порядку конъюнкция и ее окрестности S₁ и S₂ в д. н. ф. = \(∨^t_{j = 1}''_j) и проверяется соотношение

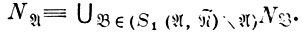
Если оно выполнено, то отметка (Δ, Δ) над заменяется на (1, Δ) и (i + 1)-й шаг А - алгоритма заканчивается. Если оно не выполнено, то проверяется, можно ли N представить в виде M₁ ∪ M₂, где М₁ - множество, регулярное относительно (, ), а М₂ - множество первого типа относительно (, ). Если N можно представить в таком виде, то отметка (Δ, Δ) над заменяется на отметку (Δ, 1), и (i + 1)-й шаг А - алгоритма заканчивается; если - нельзя, то описанная процедура применяется ко второй по порядку конъюнкции, и т. д. Если при этом ни у одной из конъюнкций отметка не изменится, то после просмотра всех конъюнкций работа A - алгоритма заканчивается.

Если за д. и. ф. принять сокращенную д. н. ф. _f функции f, то все конъюнкции, получившие в алгоритме отметку (Δ, 1), не входят ни в одну минимальную д. н. ф. функции f; они удаляются из _f . Конъюнкции, полупившие отметку (1, Δ), входят во все минимальные д. н. ф. функции f. Рассматривались также различные частные случаи A - алгоритма.

Кольцевой алгоритм расставляет над конъюнкциями информационные отметки (ω₁, ω₂), значение к-рых то же, что и в А - алгоритме. На каждом шаге кольцевой алгоритм использует конъюнкции, входящие в окрестность k-го порядка нек-рой конъюнкции, и их информационные отметки. Ниже излагается упрощенный вариант этого алгоритма. В полном виде кольцевой алгоритм - наилучший в классе локальных алгоритмов со специальной памятью по окрестностям S_k (, ) - Описанные выше алгоритмы являются частными случаями общего кольцевого алгоритма. Если

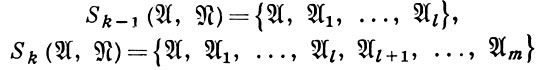
и

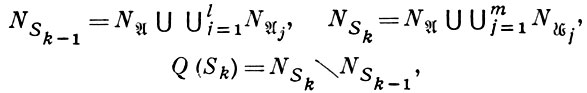
то каждому подмножеству N ⊆ Q(S_k) сопоставляется не всюду определенная булева функция f(x₁, ..., x_n), множество М₁^f единиц к-рой есть N_Sk \N, а множество M₀^f нулей есть E_n \N_Sk ; на множестве N функция f не определена. Множество таких функций обозначается через F_k (). До начала работы алгоритма все конъюнкции из рассматриваемой д. н. ф. имеют отметку (Δ, Δ). Если выполнены i шагов и отметку (1, Δ) получили конъюнкции '₁, ..., '_s, а отметку (Δ, 1) - конъюнкции ''₁, ..., ''_t, то (i + 1)-й шаг состоит в следующем. Упорядочивают нек-рым способом конъюнкции изд. н. ф. Если д. н. ф. \(∨^s_{j = 1}'_j ∨ ∨^t_{j = 1}''_j) пустая, то алгоритм заканчивает свою работу. В противном случае после упорядочения к.-л. способом всех конъюнкций этой д. н. ф. для конъюнкции , являющейся первой из них, и для каждой функции f из множества F_k () находятся все д. н. ф., реализующие f на ее области определения, к-рые составлены из конъюнкций окрестности S_k (, ) и содержат по сравнению с другими такими д. н. ф. наименьшее число символов переменных. Среди них выделяются все те д. н. ф., к-рые, во-первых, не содержат конъюнкций ''₁, ..., ''_t и, во-вторых, содержат все конъюнкции '_j, j = 1, 2, ..., s, удовлетворяющие условию N_'j ∩ (N_Sk \N) = ∅. Если для всех f из () конъюнкция входит во все выделенные д. н. ф., то отметка (Δ, Δ) над заменяется на отметку (1, Δ) и (i + 1)-й шаг алгоритма заканчивается. Если не входит ни в одну из выделенных д. н. ф., то отметка (Δ, Δ) заменяется на отметку (Δ, 1) и (i + 1)-й шаг алгоритма заканчивается. В остальных случаях описанная процедура применяется ко второй по порядку конъюнкции и т. д. Если ни у одной из конъюнкций не удается изменить отметку, то на (i + 1)-м шаге работа алгоритма заканчивается. Все конъюнкции, получившие в кольцевом алгоритме над сокращенной д. н. ф. _f функции f отметки (1, Δ) (соответственно (Δ, 1)), входят во все минимальные д. н. ф. (соответственно не входят ни в одну минимальную д. н. ф.) функции f. Результат применения описанных выше алгоритмов не зависит от способа упорядочения конъюнкций в д. н. ф.

Задача выделения всех конъюнкций, входящих хотя бы в одну и не входящих ни в одну минимальную д. н. ф., не может быть решена алгоритмами, работающими с S_k (, ) при k, ограниченных или недостаточно быстро растущих с ростом n числа переменных. Ситуация не изменится, если к запоминаемым в алгоритме свойствам P₁, Р₂ добавить ограниченное или недостаточно быстро растущее с ростом n множество свойств.

Лит. : [1] Яблонский С. В., Функциональные построения в k-значной логике, 1958 («Тр. Матем. ин-та АН СССР», т. 51); [2] Журавлев Ю. И., «Проблемы кибернетики», 1962, в. 8, с. 5-44; [3] Quinе W. V., «Аmеr. Math. Monthly», 1959, v. 66, № 9, p. 755-60.

Ю. И. Журавлев.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.