БУЛЕВЫХ ФУНКЦИЙ МЕТРИЧЕСКАЯ ТЕОРИЯ

Расстановка ударений: БУ`ЛЕВЫХ ФУ`НКЦИЙ МЕТРИ`ЧЕСКАЯ ТЕО`РИЯ

БУЛЕВЫХ ФУНКЦИЙ МЕТРИЧЕСКАЯ ТЕОРИЯ - направление, связанное с изучением числовых характеристик и метрич. свойств булевых функций. Основные разделы этой теории посвящены исследованию свойств «почти всех» булевых функций (см. Булевых функций минимизация), свойств совокупности всех булевых функций данного числа переменных и специальных подклассов булевых функций. Кроме того, изучается строение областей истинности булевых функций с помощью числовых характеристик, появившихся в основном в задачах, связанных с минимизацией булевых функций и теорией локальных алгоритмов. Этими характеристиками являются размерность и протяженность функции.

Пусть N_{f(x1, ..., xn)} - множество вершин единичного n-мерного куба, на к-рых функция f(x₁, ..., x_n) равна единице. Рассмотрим все максимальные интервалы функции f(x₁, ..., x_n) и выделим среди них интервал наибольшей размерности r. Величина r наз. размерностью функции f(x₁, ..., x_n) и обозначается через Dim f(x₁, ..., x_n). С помощью размерности оцениваются отношения сложностей самой сложной тупиковой и кратчайшей дизъюнктивных нормальных форм (д. н. ф.) функции f (см. Булевых функций нормальные формы). Сверху это отношение оценивается величиной 2^{Dim f} . В то же время для «почти всех» булевых функций имеет место неравенство

Dim f(x₁, ..., x_n) ≤ [log₂ n] + 1.

При решении задачи минимизации булевых функций представляет интерес вычисление размерности «типичных» максимальных интервалов. Доказано, что «почти все» максимальные интервалы «почти всех» булевых функций f(x₁, ..., x_n) имеют размерность, близкую к log₂ log₂ n.

Пусть S_k (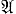, f) - главная окрестность k-го порядка (см. Алгоритм локальный) элементарной конъюнкции 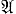, входящей в сокращенную д. н. ф. 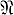_f функции f, и к (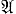, f) - минимальное значение порядка окрестности, при к-ром S_k (, f) включает в себя все элементарные конъюнкции, входящие в сокращенную д. н. ф. Величина

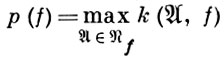
наз. протяженностью функции f. Для «почти всех» булевых функций

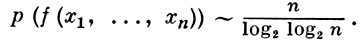
Пусть

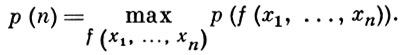
Известно, что величина р (n) реализуется на булевой функции специального вида, называемой цепью. Функция ψ (x₁, ..., x_n) наз. цепью, если множество единиц этой функции можно представить в виде последовательности α̃₁, ..., α̃_q такой, что ρ (α̃_i, α̃_{i + 1}) = 1, где ρ - расстояние Хемминга (см. Код); расстояние между другими парами α̃_r, α̃_s (может быть, за исключением пары (α̃₁, α̃_q)) больше единицы, и в множестве единиц функции ψ не содержится целиком ни один интервал размерности 2. Протяженность цепи ψ равна q - 1. Поэтому задача вычисления р(n) сводится к построению в n-мерном единичном кубе цепи с максимальным q. Прямым построением таких цепей доказано, что

c₁ ⋅ 2ⁿ < p(n) < c₂ ⋅ 2ⁿ,

где c₁, с₂ - константы. Построение замкнутых цепей (циклов), т. е. цепей, у к-рых ρ (α̃₁, α̃_q) = 1, с максимальной мощностью множества N_ψ является важной составной частью доказательства теоремы о невычислимости свойств конъюнкций «входить в минимальные или кратчайшие д. н. ф. » в классе локальных алгоритмов.

Следующий результат выясняет строение областей истинности «почти всех» булевых функций. Множество М вершин n-мерного единичного куба наз. связным, если для всякой точки α̃ ∈ М существует точка β̃ из М такая, что ρ (α̃, β̃) = 1 Точка α̃ в множестве М наз. изолированной, если для всех β̃ таких, что ρ (α̃, β̃) = 1, выполнено условие: β̃ ∉ М. Имеет место следующее утверждение: у «почти всех» булевых функций f(x₁, ..., x_n) множество единиц N_{f(x1, ..., xn)} разбивается на сумму одного связного множества и нек-рого множества изолированных тояек. При этом мощность связного множества не меньше 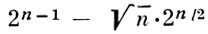- const ⋅ log₂ n, а число изолированных точек не превосходит const ⋅ log₂ n.

С результатами по вычислению протяженности «почти всех» булевых функций тесно связаны результаты по вычислению радиусов и диаметров графов, порождаемых булевыми функциями. Графом G(f), порожденным булевой функцией f, наз. граф, вершинами к-рого являются точки множества N_f, а ребрами - пары точек множества N_f, расстояние Хэмминга между к-рыми равно единице. Расстояние r_G (α̃, β̃) между вершинами α̃ и β̃ графа G(f) определяется как длина минимальной цепи, связывающей α̃ и β̃ (предполагается, что вершины #945;̃ и β̃ принадлежат одной компоненте связности графа G(f)). Отклоненноетью вершины α̃ в графе G (f) наз. величина l(α̃) = max r_G (α̃, β̃), где максимум берется по всем вершинам G, принадлежащим вместе с α̃ к одной компоненте связности. Радиусом компоненты связности К графа G наз. число 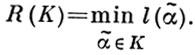. Величина R(G) = mах R (К), где максимум берется по всем компонентам связности графа G, наз. радиусом графа G. Диаметром графа G наз. число D (G) = mах r_G (α̃, β̃), где максимум берется по всем парам вершин α̃, β̃, принадлежащим одной компоненте связности. Для «почти всех» булевых функций f(x₁, ..., x_n) величины B(G) и D (G) таковы, что n - 2 ≤ R(G(f)) ≤ n - 1 и D(G(f)) = n - l.

Из результатов, относящихся к вычислению числовых характеристик отдельных классов булевых функций, выделяются результаты, относящиеся к монотонным булевым функциям. Пусть α̃ = (α̃₁ α̃₂ ...α̃_n), β̃ = (β̃₁ β̃₂ ...β̃_n) - бинарные наборы. Говорят, что α̃ ≤ β̃, если α̃_i, ≤ β̃_i, i = 1, 2, ..., n. Булева функция наз. монотонной, если из соотношения α̃ ≤ β̃ следует, что f(α̃) ≤ f(β̃). Представляет интерес определение точного числа ψ (n) различных монотонных булевых функций от переменных x₁, ..., x_n . Это число известно лишь для небольших значений n. Известно также асимптотич. равенство

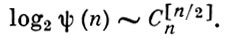
Большое число приложений при решении дискретных экстремальных задач имеет задача оптимальной расшифровки монотонной булевой функции. Пусть задан алгоритм А, позволяющий вычислять монотонную булеву функцию f(x₁, ..., x_n) в каждой точке α̃. Если в процессе вычислений установлено, что f(α̃) = 1 для нек-рой точки α̃, то f(β̃) = 1 для всех β̃ ≥ α̃. При f(α̃) = 0 функция f известна (равна нулю) во всех точках β̃ ≤ α̃. Поэтому для расшифровки, т. е. полного восстановления функции f, алгоритм А должен вычислить ее значения лишь в нек-ром множестве точек. Пусть m(f) обозначает минимальное число точек, в к-рых достаточно вычислить f(x₁, ..., x_n) для полного восстановления f. Пусть

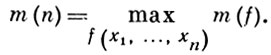
Величина m (n) удовлетворяет асимптотич. равенству:

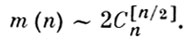
Оценка для m (f) может быть понижена, если известна дополнительная информация о монотонной булевой функции.

С задачей расшифровки монотонных булевых функций связана задача вычисления числовых характеристик совокупностей существенных переменных не всюду определенных булевых функций, т. е. функций, заданных на нек-ром подмножестве множества вершин единичного n-мерного куба. Совокупность переменных x_i1, ..., x_ik . наз. существенной для не всюду определенной булевой функции F(x₁, ..., x_n), если {x_i1, ..., x_ik} ⊆ {x₁, ..., x_n} и существует не всюду определенная булева функция φ (x_i1, ..., x_ik) такая, что F(x₁, ..., x_n) ≡ φ (x_i1, ..., x_ik) на всей области определения F. Существенная совокупность наз. тупиковой для F, если никакая истинная часть этой совокупности не является существенной для F.

У каждой всюду определенной булевой функции имеется единственная тупиковая совокупность переменных. Для не всюду определенных булевых функций строение совокупностей существенных переменных отличается большим разнообразием. Пусть Σ - система подмножеств множества {x₁, ..., x_n}, удовлетворяющая условию: если S ∈ Σ и S' - произвольное подмножество множества {x₁, ..., x_n}, то S ∪ S' ∈ Σ. Тогда существует не всюду определенная булева функция F_Σ (x₁, ..., x_n) такая, что система существенных для F_Σ наборов переменных есть Σ. Пусть t_F (n) - число различных тупиковых наборов для F(x₁, ..., x_n) и

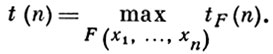
Известно, что

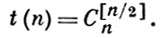
Алгоритм построения всех тупиковых совокупностей переменных для F(x₁, ..., x_n) имеет максимальную трудоемкость 2С^[n/2]_n, причем этот максимум достигается (здесь единицей трудоемкости считается трудоемкость проверки, является ли данная совокупность переменных существенной для F).

К Б. ф. м. т. относят также задачи вычисления характеристик, связанных с задачей минимизации булевых функций.

Лит. : [1] Глаголев В. В., «Проблемы кибернетики», 1967, в. 19, с. 75-94; [2] Журавлев Ю. И., «Проблемы кибернетики», 1964, в. 11, с. 271-75; [3] Коробков В. К., «Проблемы кибернетики», 1965, в. 13, с. 5-28; [4] Сапоженко А. А., сб. «Дискретный анализ», 1967, в. 10, с. 91-119; [5] его же, «Докл. АН СССР», 1968, т. 180, № 1, с. 32-35; [6] Kleitman D., «Рrос. Amer. Math. Soc. », 1969, v. 21, № 3, p. 677-82.

Ю. И. Журавлев.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.