БУЛЕВОЗНАЧНАЯ МОДЕЛЬ

Расстановка ударений: БУЛЕВОЗНА`ЧНАЯ МОДЕ`ЛЬ

БУЛЕВОЗНАЧНАЯ МОДЕЛЬ - модель, определяемая следующим образом. Пусть Ω - сигнатура нек-рого языка L 1-й ступени с одним сортом переменных, т. е. Ω - множество символов функций и предикатов. Б. м. наз. тройка M = (B_M, V_M, Ω_M), где B_M - невырожденная булева алгебра, V_M - непустое множество и Ω_M - функция, определенная на Ω и такая, что

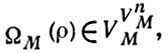
если ρ есть n-местный функциональный символ, и

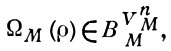
если ρ есть n-местный предикатный символ. Запись X^Y обозначает множество всех функций, определенных на Y со значениями в X и Xⁿ = Х^{{m|m < n}}, где n ≥ 0-натуральное число. Булева алгебра наз. множеством истинностных значений модели М. Множество V_M наз. универсумом модели М. Б. м. М наз. также В-моделью, если множество истинностных значений есть булева алгебра В, В_M = В. Если булева алгебра В двухэлементна (т. е. B = {0, 1}), то H-модель М есть классическая двузначная модель.

Пусть L_M - язык, пополненный новыми индивидными константами: для каждого v ∈ V_M своя индивидная константа v. Пусть М есть B-модель и В = (В; 0, 1, -, ∪, ∩) - полная булева алгебра. Тогда нижеследующие равенства 1)-8) определяют значение ||e||_M каждого замкнутого выражения е (т. е. формулы или терма без свободных переменных) языка L_M :

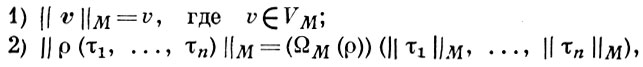
где τ₁, ..., τ_n - замкнутые термы и ρ есть n-местный функциональный или предикатный символ;

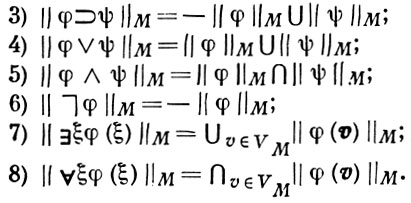
Соотношения 1)-8) определяют значение ||e||_M и для некоторых неполных булевых алгебр; надо только, чтобы существовали бесконечные объединения и пересечения в 7) и 8). Понятие Б. м. можно ввести и для языков со многими сортами переменных. В этом случае для каждого сорта переменных будет своя область изменения V_M .

Замкнутая формула φ наз. истинной в B-модели М (M⊨ φ), если

||φ||_M = 1.

B-модель М наз. моделью теории Т, если М⊨ φ для каждой аксиомы ф теории Т. Если h есть гомоморфизм булевой алгебры В на булеву алгебру В', сохраняющий бесконечные объединения и пересечения, то существует B'-модель М' такая, что

||φ ||_M' = h (||φ ||_M)

для каждой замкнутой формулы φ языка L_M . В случае, если универсум модели М счетен, то существует гомоморфизм h в булеву алгебру {0, 1}, позволяющий переделать модель М в классическую двузначную модель М' такую, что

М ⊨ φ → М' ⊨ φ.

Доказано, что теория Т непротиворечива тогда и только тогда, когда она имеет Б. м. На этой теореме основано применение теории Б. м. к вопросам непротиворечивости аксиоматич. теорий.

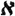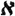Если Б. м. теории Т строится средствами другой аксиоматич. теории S, то получается результат о непротиворечивости теории Т относительно S. Так, напр., результат П. Коэна (P. Cohen) о непротиворечивости теории ZF + (2^₀ > ₁) относительно ZF можно получить построением соответствующей Б. м. средствами системы ZF (см. Вынуждения метод). Построение коэновского отношения вынуждения р|| - φ равносильно построению такой Б. м. М, что

||φ ||_M = {p: p ||- ¬¬ φ }.

Лит. : [1] Расёва Е., Сикорский Р., Математика метаматематики, пер. с англ., М., 1972; [2] Йех Т., Теория множеств и метод форсинга, пер. с англ., М., 1973; [3] Тakеuti G., Zаring W. M., Axiomatic set theory, N. Y. [a. o.], (1973); [4] Maнин Ю. И., в сб. : Итоги науки и техники. Современные проблемы математики, т. 5, М., 1975, с. 5-72.

В. Н. Гришин.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.