БУЛЕВО КОЛЬЦО

Расстановка ударений: БУ`ЛЕВО КОЛЬЦО`

БУЛЕВО КОЛЬЦО - ассоциативное кольцо K, все элементы к-рого идемпотентны, т. е. х² = х для любого х ∈ К. Любое Б. к. K ≠ 0 коммутативно и является подпрямой суммой полей Z₂ из двух элементов. При этом х + х = 0 для всех х ∈ К. конечное Б. к. K ≠ 0 является прямой суммой полей Z₂ и потому имеет единицу.

Б. к. - это кольцевой вариант булевых алгебр, а именно: любая булева алгебра является Б. к. с единицей относительно операций сложения и умножения, определяемых правилами

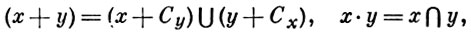
где С_x - дополнение элемента х. Нуль и единица кольца совпадают с нулем и единицей алгебры. Обратно, любое Б. к. с единицей есть булева алгебра относительно операций x ∪ у = х + у + ху, x ∩ y = x - y, С_x = 1 + х.

Лит.: [1] Stone М. Н., «Trans. Amer. Math. Soc. », 1936, v 40 № 1, p. 37-111; [2] Жeгалкин И. И., «Матем. сб. », 1927, т. 34, в. 1, с. 9-28; [3] Владимиров Д. А., Булевы алгебры, М., 1969; [4] Сикорский Р., Булевы алгебры, пер. с англ., М., 1969.

Ю. М. Рябухин.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.