БУЛЕВА ФУНКЦИЯ

Расстановка ударений: БУ`ЛЕВА ФУ`НКЦИЯ

БУЛЕВА ФУНКЦИЯ, функция алгебры логики, - функция, аргументы к-рой, равно как и сама функция, принимают значения из двухэлементного множества (обычно {0, 1}). Б. ф. являются одним из основных объектов дискретной математики, в особенности тех ее разделов, к-рые входят в математич. логику и математич. кибернетику. Б. ф. возникли при математич. постановке задач логики и были названы по имени Дж. Буля (G. Boole), положившего начало применению математики в логике (сер. 19 в. ; см. Алгебра логики).

Одной из таких задач является построение алгебры высказываний. Для этого каждому высказыванию приписывается одно из двух значений 0 или 1 (играющие, соответственно, роль «лжи» и «истины»), и тогда основные логич. связки «и», «или», «не», «если..., то» и др. можно рассматривать, соответственно, как «элементарные» Б. ф. : х&у, х ∨ у, х¯, х → у и т. д. Тем самым значение любого сложного высказывания, построенного с помощью основных логич. связок из заданных высказываний, является Б. ф. от значений этих высказываний. Такая Б. ф. представляет собой суперпозицию элементарных Б. ф., соответствующих логич. связкам, входящим в сложное высказывание. Позднее выяснилось, что язык Б. ф. удобен для описания функционирования дискретных управляющих систем таких, как контактные схемы, схемы из функциональных элементов, логич. сети и др. Эти управляющие системы строятся по определенным правилам из нек-рых исходных элементов подобно тому, как сложные высказывания строятся из элементарных. Правила построения указанных управляющих систем, а также функционирование исходных элементов таковы, что функционирование сложных управляющих систем может быть описано с помощью Б. ф. Б. ф. используются также в нек-рых задачах целочисленного программирования, к-рые сводятся к решению систем булевых уравнений вида

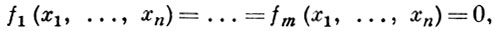
где f_i - Б. ф., i = 1, 2, ..., m. Существуют и другие возможности применения Б. ф. в дискретной математике, благодаря чему изучение Б. ф. представляет самостоятельный интерес.

При решении различных задач, связанных с Б. ф., существенным моментом является способ задания Б. ф. Имеется целый ряд таких способов: таблицы, формулы, специальные классы формул, наз. нормальными формами (см. Булевых функций нормальные формы), подмножества вершин n-мерного единичного куба и др. В последнем случае каждый набор длины n значений аргументов (0 или 1) рассматривается как вершина n-мерного единичного куба, и тогда Б. ф. от n аргументов может быть задана с помощью подмножества вершин, в к-рых эта функция принимает значение 1. Это подмножество, выписанное в виде матрицы, строками к-рой являются наборы значений аргументов Б. ф., наз. булевой матрицей. В том случае, когда Б. ф. описывает функционирование управляющих систем, последнюю также можно рассматривать как средство задания Б. ф. Обычно говорят, что эта управляющая система реализует данную Б. ф. С реализацией Б. ф. теми или иными видами управляющих систем связан большой круг задач таких, как задачи синтеза, минимизации, задачи контроля и надежности и др. Другой круг задач возникает при изучении свойств и классов Б. ф. в связи с различными способами задания; это - изучение метрич. характеристик различных классов нормальных форм Б. ф. и связанных с ними геометрич. свойств n-мерного единичного куба (см. Булевых функций метрическая теория), а также различных алгебр Б. ф. (см. Многозначная логика, Эквивалентные преобразования). Система всех классов Б. ф., замкнутых относительно суперпозиций, была описана Э. Постом (Е. Post). Она образует счетно бесконечную структуру с пятью максимальными (предполными) классами.

В нек-рых случаях возникает необходимость рассматривать частичные, т. е. не всюду определенные, Б. ф., для к-рых перечисленные задачи имеют характерную специфику.

Лит. : [1] Новиков П. С., Элементы математической логики, 2 изд., М., 1973; [2] Яблонский С. В., Гаврилов Г. П., Кудрявцев В. Б., Функции алгебры логики и классы Поста, М., 1966.

В. Б. Кудрявцев.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.