
БУЛЕВА АЛГЕБРА
Расстановка ударений: БУ`ЛЕВА А`ЛГЕБРА
БУЛЕВА АЛГЕБРА, булева решетка, - частично упорядоченное множество специального вида. Б. а. наз. дистрибутивная решетка (дистрибутивная структура), имеющая наибольший элемент 1 - единицу Б. а., наименьший элемент 0-нуль Б. а. и содержащая вместе с каждым своим элементом х его дополнение - элемент Сх, удовлетворяющий соотношениям
sup {х, Сх} = 1, inf {х, Сх} = 0.
Операции sup и inf обозначаются обычно знаками ∨ и ∧, а иногда ∪ и ∩, чем подчеркивается их сходство с теоретико-множественными операциями объединения и пересечения. Вместо Сх иногда пишут х¯, х', - х. Дополнение всякого элемента в Б. а. единственно.
Б. а. может определяться и иначе, а именно, как непустое множество с операциями С, ∨, ∧, удовлетворяющими аксиомам:
1) х ∨ у = у ∨ х, х ∧ у = у ∧ х;
2) х ∨ (у ∨ z) = (x ∨ у) ∨ z, х ∧ (у ∧ z) = (x ∧ у) ∧ z;
3) (х ∧ у) ∨ у = у, (х ∨ у) ∧ y = y;
4) х ∧ (y ∨ z) = (х ∧ y) ∨ (х ∧ z), х ∨ (у ∧ z) = (x ∨ у) ∧ (х ∨ z);
5) (х ∧ Сх) ∨ у = у, (x ∨ Сх) ∧ у = у.
При таком подходе упорядочение не предполагается заранее заданным, а вводится условием: x ≤ y тогда и только тогда, когда х = х ∧ у.
Возможны и другие аксиоматики. В аксиомах Б. а. отражена аналогия между понятиями «множества», «события», «высказывания». Отношение порядка в Б. а. может быть (в зависимости от выбора интерпретации) истолковано как теоретико-множественное включение, как причинное следование для событий, как логич. следование для высказываний и т. д.
Кроме основных операций С, ∨, ∧, в Б. а. могут быть определены и другие, среди к-рых особенно важна операция симметрической разности:
х + 2 у = (х ∧ Су) ∨ (у ∧ Сх)
(пишут также хΔ у, |х - у|).
Всякая Б. а. есть булево кольцо с единицей относительно операций + 2 («сложение») и ∧ («умножение»); любое булево кольцо с единицей можно рассматривать как Б. а.
Б. а. возникли в трудах Дж. Буля [1], [2] как аппарат символич. логики. В последующем они нашли широкое применение в различных разделах математики - в теории вероятностей, топологии, функциональном анализе и др. В основе приложений Б. а. к логике лежит интерпретация элементов Б. а. как высказываний (см. Алгебра логики); при этом дополнение Сх истолковывается как отрицание высказывания х, а операции ∧ и ∨ - как конъюнкция и дизъюнкция. К логике близка и другая область применения Б. а. - теория контактных схем. Б. а. используются при обосновании теории вероятностей. Поле событии, изучаемое в теории вероятностей, есть Б. а. ; при этом неравенство x ≤ y означает, что событие х влечет событие у; соответственно с этим истолковываются нуль Б. а., единица Б. а. и булевы операции ∨, ∧, С.
Пример Б. а. - упорядоченная по включению система всех подмножеств к.-л. фиксированного множества Q. Такая Б. а. обозначается 2Q ; ее нулем служит пустое множество, единицей - само множество Q. Дополнение элемента х есть множество Q\х; булевы операции ∨ и ∧ совпадают соответственно с объединением и пересечением.
Вместо подмножеств множества Q удобно рассматривать их характеристич. функции. Система XQ всех таких функций при естественном упорядочении оказывается Б. а., изоморфной Б. a. 2Q . Операции ∨, ∧, С. + 2 истолковываются в такой Б. а. следующим образом:
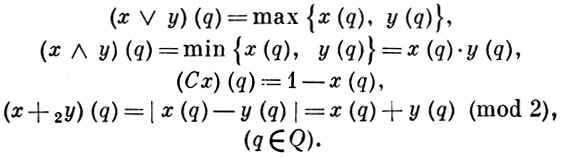
Особенно важны случаи:
1) Q = Qn = {1, 2, ..., n).
Характеристич. функции подмножеств в данном случае суть «двоичные символы» вида
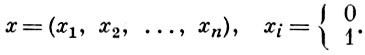
Их число равно 2n . При n = 1 получается двухэлементная Б. а., состоящая только из нуля и единицы.
2) Q = XQn .
В этом случае элементами XQ будут всевозможные функции, заданные на системе всех двоичных символов длины n и принимающие только значения 0 и 1. Их наз. булевыми функциями от n переменных. Всякая правильно построенная формула логики высказываний определяет нек-рую булеву функцию, причем совпадение функций означает эквивалентность формул.
При нек-рых условиях множество Е элементов Б. а. X само оказывается Б. а. относительно индуцированного из X порядка. Так будет, в частности, в следующих случаях:
а) Е - главный идеал, т. е. множество вида {х ∈ Х|х ≤ u}; роль единицы здесь играет элемент u;
б) Е - подалгебра Б. а. X. Это означает, что из x, у ∈ Е следует х ∨ у, х ∧ у, Сх ∈ Е. Нулем и единицей новой Б. а. служат нуль и единица исходной Б. а. Особенно важны подалгебры Б. a. 2Q ; их наз. алгебрами множеств. Всякое множество Е ⊂ Х порождает нек-рую подалгебру - наименьшую подалгебру, содержащую Е.
Среди отображений Б. а. особую роль играют гомоморфизмы Б. а., то есть отображения, перестановочные с булевыми операциями. Биективный гомоморфизм Б. а. является изоморфизмом Б. а. Если Б. а. X порождена множеством Е, то для того чтобы всякое отображение множества Е в произвольную Б. а. допускало продолжение до гомоморфизма, необходимо и достаточно, чтобы Е было независимым множеством, т. е. чтобы все элементы вида
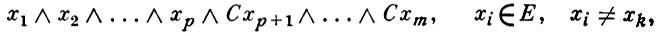
были отличны от нуля. Б. а., порожденная независимой системой, наз. свободной Б. а.
Пример свободной Б. а. - рассмотренная выше алгебра булевых функций от n переменных. Ее независимыми образующими являются функции
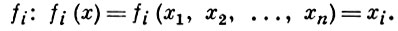
Теорема Стоуна: всякая Б. а. X изоморфна нек-рой алгебре множеств, а именно, алгебре всех открыто-замкнутых множеств вполне несвязного бикомпакта 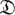 (X), определяемого с точностью до гомеоморфизма. Этот бикомпакт наз. стоуновским бикомпактом. Гомоморфизму Б. а. X в Б. а. Y соответствует топологич. вложение
(X), определяемого с точностью до гомеоморфизма. Этот бикомпакт наз. стоуновским бикомпактом. Гомоморфизму Б. а. X в Б. а. Y соответствует топологич. вложение 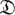 (Y) в
(Y) в 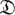 (X); подалгебре Б. а. X соответствует непрерывный образ бикомпакта
(X); подалгебре Б. а. X соответствует непрерывный образ бикомпакта 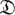 (X). Стоуновский бикомпакт свободной Б. а. есть двоичный дисконтинуум.
(X). Стоуновский бикомпакт свободной Б. а. есть двоичный дисконтинуум.
Б. а. X наз. полной, если всякое множество Е ⊂ Х имеет верхнюю грань sup Е и нижнюю грань inf Е. Это равносильно экстремальности бикомпакта 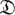 (X) (см. Экстремально несвязные пространства). Подалгебры полной Б. а., содержащие вычисленные в X грани всех своих подмножеств, наз. правильными подалгебрами. Вес Б. а. X есть наименьшая мощность вполне порождающего множества, т. е. множества, не содержащегося ни в какой правильной подалгебре, отличной от X. Если веса всех ненулевых главных идеалов совпадают, то Б. а. наз. однородной; такая Б. а. всегда содержит вполне порождающее независимое множество. Другими словами, полная однородная Б. а. «натянута» на свободную Б. а. Изучение произвольной Б. а. легко сводится к изучению однородных Б. а. Неполная Б. а. может быть многими способами пополнена, т. е. вложена в качестве подалгебры в нек-рую полную Б. а.
(X) (см. Экстремально несвязные пространства). Подалгебры полной Б. а., содержащие вычисленные в X грани всех своих подмножеств, наз. правильными подалгебрами. Вес Б. а. X есть наименьшая мощность вполне порождающего множества, т. е. множества, не содержащегося ни в какой правильной подалгебре, отличной от X. Если веса всех ненулевых главных идеалов совпадают, то Б. а. наз. однородной; такая Б. а. всегда содержит вполне порождающее независимое множество. Другими словами, полная однородная Б. а. «натянута» на свободную Б. а. Изучение произвольной Б. а. легко сводится к изучению однородных Б. а. Неполная Б. а. может быть многими способами пополнена, т. е. вложена в качестве подалгебры в нек-рую полную Б. а.
Полная Б. а. наз. нормированной, если на ней определена действительная функция μ (мера), обладающая свойствами: 1) μ (х) > 0 при х ≠ 0; 2) если Е ⊂ Х и х ∧ у = 0 при х, у ∈ Е, х ≠ у, то
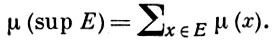
В теории вероятностей, где нормированные Б. а. особенно важны, обычно предполагают, что μ (1) = 1. При этом значение μ (х) интерпретируется как вероятность события х. На нормированные Б. а. в основном переносится классическая теория меры и интеграла. Для нормированных Б. а. имеется полная классификация (см. [4], [5], [7]). В частности, для однородных нормированных Б. а. единственным инвариантом является вес. Не всякая Б. а. может быть нормирована. Известны различные условия существования меры, однако они далеко не исчерпывают проблемы нормируемости.
Б. а. может быть наделена различными топологиями. Особенно важна так наз. (о)-топология, к-рая в случае нормированной Б. а. метризуема и соответствует метрике
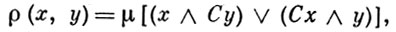
а для Б. а. вида 2Q совпадает с тихоновской топологией. В самом общем случае может не существовать никакой топологии, хорошо согласованной с порядком в Б. а.
Лит. : [1] Вооlе G., The mathematical analysis of logic, Camb. - L., 1847; [2] eго же, An investigation of the laws of thought, L., 1 854; [3] Сикорский Р., Булевы алгебры, пер с англ., М., 1969; [4] Владимиров Д. А., Булевы алгебры, М., 1969; [5] Halmos P., Lectures on Boolean algebras, Toronto - N. Y. - L., [1963]; [6] Pасёвa E., Сикорский Р., Математика метаматематики, пер. с англ., М 1972; [7] Stone М. Н., «Trans. Amer. Math. Soc. », 1936, v. 40, № 1, p. 37-111; [8] Биpкгоф Г., Теория структур, пер. с англ., М., 1952; [9] Hermes Н., Einfuhrung in die Verbandstheorie, В. - Gott. - Hdlb., 1955; [10] Колмогоров A. H., Algebres de Boole metriques completes, в кн. : VI Zjazd, Mathematykow Polskich, Krakow, 1950; [11] Данфорд H., Шварц Дж., Линейные операторы, [ч. 3] - Спектральные операторы, пер. с англ., М., 1974; [12] Кakutаni S., «Аnn. Math. », 1941, v. 42, ser. 2, p. 523-37, 994-1024; [13] Мahаram D., «Рrос. Nat. Acad. Sci. U. S. A. », 1942, v. 28, p. 108-11; [14] Mакки Дж., Лекции по математическим основам квантовой механики, пер. с англ., М., 1965; [15] Иосида К., Функциональный анализ, пер. с англ., М., 1967; [16] Куратовский К., Топология, т. 2, пер. с англ., М., 1969.
Д. А. Владимиров.
Источники:
- Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'