БРУННА-МИНКОВСКОГО ТЕОРЕМА

Расстановка ударений: БРУ`ННА-МИНКО`ВСКОГО ТЕОРЕ`МА

БРУННА-МИНКОВСКОГО ТЕОРЕМА: пусть K₀ и K₁ - выпуклые множества, n-мерного евклидова пространства, К_λ, λ ∈ [0, 1] (линейная комбинация K₀ и К₁) - множество точек, делящих отрезки с концами в любых точках множеств K₀ и К₁ в отношении λ /(1 - λ), V(λ) - корень n-й степени из объема множества К_λ ; тогда V(λ) - вогнутая функция от λ, т. е. для любых λ₁, λ₂, ρ ∈ [0, 1] выполняется неравенство

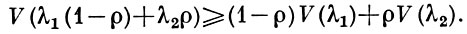
Функция V(λ) линейна (и тогда неравенство обращается в равенство) в том и только в том случае, когда K₀ и К₁ гомотетичны. Б.-М. т. обобщается на линейные комбинации нескольких выпуклых множеств. Б.-М. т. используется для решения эктремальных задач и задач единственности. Б.-М. т. установлена Г. Брунном (Н. Brunn) в 1887, уточнена и дополнена Г. Минковским (Н. Minkowski) в 1897.

Лит. : [1] Буземан Г., Выпуклые поверхности, пер. с англ., М., 1964; [2] Xадвигер Г., Лекции об объеме, площади поверхности и изопериметрии, пер. с нем., М., 1966.

М. И. Войцеховский.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.