БРИО-БУКЕ УРАВНЕНИЕ

Расстановка ударений: БРИ`О-БУ`КЕ УРАВНЕ`НИЕ

БРИО-БУКЕ УРАВНЕНИЕ - обыкновенное дифференциальное уравнение

x^m y' = f(x, у), (1)

где m - целое положительное число, функция f аналогична при х = у = 0, f'_y (0, 0) ≠ 0, f(0, 0) = 0. Ш. Брио и Т. Буке показали [1], что всякое уравнение вида

α (z, w) w' = β (z, w),

где α (0, 0) = β (0, 0) = 0 и α и β аналитичны в начале, с помощью специальных локальных замен переменных может быть сведено к нек-рому числу уравнений вида (1). Уравнение (1) всегда (кроме случая m = 1, f'_y (0, 0) есть натуральное число) имеет единственное решение в виде формального степенного ряда

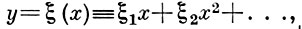
(2)

к-рый сходится для достаточно малых |x|, если m = 1, и может расходиться для всех х ≠ 0, если m > 1. Пусть в (1)

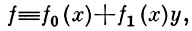
тогда для сходимости ряда (2) необходимо и достаточно выполнения m - 1 условий на коэффициенты рядов Тейлора функций f₀ и f₁, причем в эти условия входят все коэффициенты, так что наличие или отсутствие аналитич. решения у = ξ (х) уравнения (1) не может быть определено ни по какому конечному отрезку ряда Тейлора функции f. Поэтому иногда Б.-Б. у. наз. уравнение (1) с m > 1.

Лит. : [1] Вriоt С., Bouquet Т., «J. de l'Ecole polytechnique», 1856, v. 21, p. 85-132, 133-98; [2] Вieberbасh L., Theorie der gewöhnlichen Differentialgleichungen auf funktionentheoretischer Grundlage dargestellt, 2 Aufl., В., 1965; [3], Бpюно А. Д., «Тр. Моск. матем. об-ва», 1971, т. 25, с. 120-138 (Введение).

А. Д. Брюно.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.